ASTR 1210 (O'Connell) Study Guide

---

8. GRAVITATIONAL ORBITS AND SPACE FLIGHT

Space Shuttle Discovery launches on
a mission to the Space Station, 2001

"There will certainly be no lack of human pioneers when we have mastered the art of [space] flight....Let us create vessels and sails adjusted to the heavenly ether, and there will be plenty of people unafraid of the empty wastes. In the meantime we shall prepare, for the brave sky-travelers, maps of the celestial bodies." ---- Johannes Kepler (1610)

Kepler was right about the multitudes of people eager to travel into space, but it took another 350 years of technological development to build the "vessels" needed to carry them. Space travel is difficult. However, the theoretical key to space flight was discovered by Newton only 80 years after Kepler's work.

Newton's theories of dynamics and gravity provided a complete understanding of the interaction between gravitating bodies and the resulting orbits for planets and satellites. This guide first describes the nature of possible gravitational orbits and some implications of those.

Two hundred and fifty years after he died, Newton's work became the foundation of space technology, which is introduced in the second part of the guide. Space technology---rockets, the Space Shuttle, scores of robot spacecraft, the human space program---has provided most of our present knowledge of the Solar System and most of the material we will discuss in the rest of this course. Commercial space technology (e.g. GPS, communications, and remote observing satellites) is already an integral part of modern life.

The mid-20th century was the first time humans had ever sent machines beyond the Earth's atmosphere. By 2015, we had explored every large body in the Solar System out to the orbit of Pluto. Even such far-sighted thinkers as Galileo and Newton himself would never have thought that possible in the mere 400 years that had elapsed since Kepler's Laws were formulated. This was an amazing accomplishment, the greatest exploratory feat of humanity to date.

A. Newtonian Orbit Theory

Orbital Dynamics

Newton's theory can accurately predict gravitational orbits because it allows us to determine the acceleration of an object in a gravitational field.

Acceleration is the rate of change of an object's velocity.
If we know the initial position and velocity of an object, knowing its acceleration at all later times is enough to completely determine its later path of motion.
To predict the path, we simply substitute Newton's expression for F_grav for the force term in his Second Law and solve for acceleration:
a = F_grav/m
But there are major complications. The Second Law is not a simple algebraic expression. Both velocity and acceleration are rates of change (of position and velocity, respectively). Mathematically, they are derivatives. The gravitational force also changes with position. Finally, velocity, acceleration and the gravitational force all have a directionality as well as a magnitude associated with them. That is, they are "vectors".
So the Second Law is really a differential vector equation. To solve it, Newton had to invent calculus.

We don't need to know the mathematical details in order to understand the basic interaction that shapes Newtonian orbits. Take as an example the orbit of the Earth around the Sun.
Pick any location on the Earth's orbit. Represent its velocity at that location as an arrow (a vector) showing the direction and magnitude of its motion.
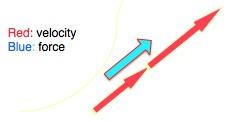
An essential element of Newtonian theory is that changes in the magnitude of the velocity vector (the speed) or in the direction of motion are both considered to be "accelerations." In the following drawings, the red arrows represent the Earth's velocity vector and the blue arrows represent the applied gravitational force. According to Newton's Second Law, the change in the velocity vector (a speed-up in the first case or a deflection of the direction of motion in the second) is in the direction of the applied force.
Starting from any location, the instantaneous velocity vector and the rate of change of that vector (the acceleration) combine to determine where the Earth will be at the next moment of time. Adding up the motion from one moment to the next traces out the orbital path.
In Newtonian gravity, the gravitational force acts radially --- i.e. along the line connecting the Earth and the Sun. Accordingly, both the acceleration and the change in the Earth's velocity vector from one moment in time to the next will also always be in the radial direction.
You might think that if the acceleration is always toward the Sun, then the Earth should fall faster and faster on a radial trajectory until it crashes into the Sun. That's exactly what would happen if the Earth were ever stationary in its orbit. In that case, the situation in the left hand drawing above (straight-line acceleration toward the Sun) would prevail.
But if the Earth's velocity vector has a component which is perpendicular to the radial direction, then in any interval in time, it will move "sideways" at the same time as it accelerates toward the Sun. If the combination of sideways motion and distance from the Sun is correct, the Earth will avoid collision with the Sun, and it will stay in permanent orbit. The animation at the right shows the situation for the Earth's (exaggerated) elliptical orbit around the Sun (here, the blue line is the velocity vector, the green line is the acceleration; click for an enlargement). Note that where the Earth is nearest the Sun, the gravitational force and inward acceleration are greatest, but the sideways motion is also greatest, which prevents us from colliding with the Sun. That motion is in accordance with Kepler's second law.
Therefore, all permanently orbiting bodies are perpetually falling toward the source of gravity but have enough sideways motion to avoid a collision.

Kinds of Gravitational Orbits

In the case of two gravitating objects (for example, the Earth and the Moon, the Sun and a planet, or the Earth and an artificial satellite), Newton found that the full solutions of his equations give the following results:

• The relative orbit is confined to a geometric plane which contains both objects.

• The shape of the orbit within the plane is a "conic section", of which there are only four types.
  • A circle
    
  • An ellipse
    
  • A parabola
    
  • A hyperbola
    See the illustration at the right.

• The orbital type is determined by the initial distance, speed (V) and direction of motion of the orbiting object, as follows:
  • Define the "escape velocity" at a given distance: V_esc(R) = √(2GM/R), where R is the separation between the two objects and M is the mass of the primary object.
    V_esc for the Earth at the Earth's surface is 25,000 mph (or 11 km/s). V_esc for the Sun at the Earth's 1 AU distance from the Sun is 94,000 mph (42 km/s).

  
• If V < V_esc, the orbit is an ellipse or circle. It is said to be "closed" or "bound". The smaller object will permanently repeat its orbital motion.

• If V ≥ V_esc, the orbit is a parabola or hyperbola. It is said to be "open" or "unbound". The smaller object escapes and does not return.

• Only specific values of velocity will yield circular or parabolic orbits. An object moving exactly at escape velocity will move on a parabola. To achieve a circular orbit an object must move at 71% of the escape velocity, and its velocity must be exactly perpendicular to the radial direction. Other combinations of velocity or direction lead to elliptical or hyperbolic orbits.

• As noted earlier, shapes and motions within the "closed" orbits for the planets satisfy all three of Kepler's Laws of planetary motion.

You can interactively explore the relation between the orbit and the initial velocity vector using the Flash animation Gravity Chaos.

Newton's Mountain

Newton illustrated orbital behavior for a simple idealized situation where a powerful cannon is fixed in position on top of a high mountain on the Earth's equator. It is allowed to fire only with its barrel parallel to the Earth's surface (see the illustration below). Since both the distance from Earth's center and the direction of initial flight are fixed, the cannonball follows an orbit that depends only on the muzzle velocity of the cannon as shown below.

The gravitational force of a spherical body like the Earth acts as though it originates from the center of the sphere, so elliptical orbits of the cannonball will have the center of the Earth at one focus. The center of the Earth lies directly under the red dot in the picture below.
(For simplicity, the diagram omits showing "orbits" where the muzzle velocity is far enough below the circular orbit velocity that the cannonball hits the surface of the Earth. Needless to say, that is the situation for all real-life cannons; but the flight paths taken before the collision do have elliptical shapes.)

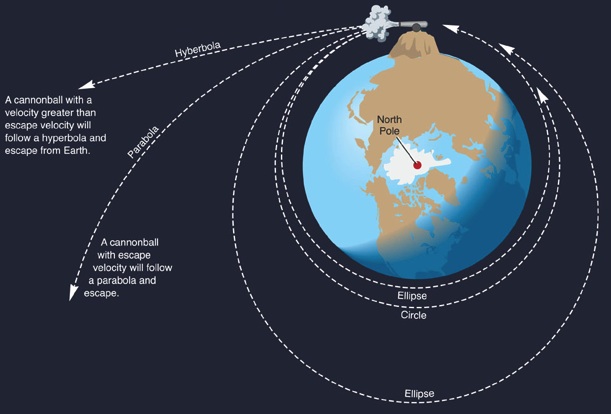
"Newton's Mountain": orbit type depends on initial velocity.
From lower to higher velocities, orbit shapes are: ellipse, circle, ellipse, parabola, hyperbola.
"Escape velocity" (which is 25,000 mph at Earth's surface) produces a parabolic orbit.

General Relativity

Much later (1915), Newton's theory was shown by Albert Einstein to be inadequate in the presence of large masses or over large distances and has been replaced by the General Theory of Relativity in such situations. Relativity theory profoundly changed our understanding of space and time, for example by demonstrating that mass and energy can affect the structure of space and time, something that Newton never contemplated. It is much more complicated mathematically than Newton's formulation. But as a practical matter, Newton's theory is an entirely satisfactory description of "everyday" gravity. Only very minor corrections to the Newtonian predictions are necessary, for example, to send spacecraft with high accuracy throughout the solar system.

General Relativity predicted important phenomena that were not foreseen in Newtonian physics, including black holes (closed regions of space-time around massive, compact objects) and gravitational waves (propagating disturbances in the structure of space-time).
The first detection of cosmic gravitational waves, generated by the merger of two very distant black holes, was announced by LIGO (the Laser Interferometer Gravitational-Wave Observatory) in February of 2016. This was one of the most difficult scientific experiments ever attempted as well as a brilliant confirmation of the validity of General Relativity.

B. Important Implications of Newtonian Orbits

"Free-Fall" Orbits

Free motion in response to gravity (in the absence of other forces) is called "free-fall" motion. Conic section orbits are all "free-fall orbits."
Remember that motion is normal in free-fall. For instance, rocket engines do not have to be on in order for spacecraft to move through space on a free-fall orbit. Spacecraft will "coast" forever on such an orbit, just as do the planets in orbit around the Sun.
Note also that free-fall orbits will depart from simple conic sections if an object is under the influence of more than one gravitating body. For instance, comets are often deflected from their Sun-dominated simple conic orbits by Jupiter's gravity (see Guide 21), and spacecraft traveling between the Earth and the Moon will not follow simple conic paths.

Free-fall orbits are independent of the mass of the orbiting object.
Another way of stating this is to say that the acceleration of all objects is the same in a given gravity field (e.g. at a given distance from the Sun or near the Earth's surface), regardless of their masses. This was first demonstrated experimentally by Galileo and was the subject of our "object drop" Puzzlah (see Study Guide 7).
The mass of the orbiting body always cancels out of the expression for acceleration under gravity. For instance, in the case of a planet orbiting the Sun, the gravitational force on the planet is directly proportional to the planet's mass; but, according to Newton's Second Law, the resulting acceleration is inversely proportional to its mass. So, mass drops out of the expression for acceleration.
This is true for all orbits under gravity. Hence, a tennis ball in space, if it were moving with the same speed and direction as the Earth at any point, would follow exactly the same orbital path as the Earth around the Sun.
Kepler's Third Law (that the orbital period of a planet around the Sun depends only on its orbital size, not on the mass of the planet) is another manifestation of this fact.

A more familiar manifestation of "free fall" these days is the phenomenon of "floating" astronauts on space missions. Even though the spacecraft is much more massive, both the astronauts and the spacecraft have identical accelerations under the external gravitational fields. They are moving on parallel free-fall orbits, so the astronauts appear to be floating and stationary with respect to the spacecraft, even though they are actually both moving at over ten thousand miles per hour in near-Earth orbit.
Here are some brief videos of free-fall on the Space Shuttle during the Astro-2 UV observatory mission in 1995: camera toss; dinner flip; tortilla catch.

Turning on a rocket engine breaks its free-fall path. Rocket engines are described under (C) below. You can think of a rocket engine in the abstract as a device for changing from one free-fall orbit to another by applying a non-gravitational force.
With its engine turned off, the motion of any spacecraft is a free-fall orbit. If the engine is on, the craft is not in free fall. For instance, the orbit of the Space Shuttle launching from the Earth will depart from a conic section until its engines turn off. An example of using a rocket engine to change from one free-fall orbit to another is shown here.

The Russian "Mir" space station (1986-2001) orbiting Earth in free-fall at an altitude of 200 miles with a velocity of 17,000 mph

Geosynchronous Orbits

According to Kepler's Third Law, the orbital period of a satellite will increase as its orbital size increases. We have exploited that fact in developing one of the most important practical applications of space technology: geosynchronous satellites.
• Spacecraft in "low" Earth orbits (less than about 500 mi), like the Mir space station (seen above) or the Space Shuttle, all orbit Earth in about 90 minutes, at 17,000 miles per hour, regardless of their mass. As seen from a given point on Earth's surface, they travel quickly across the sky and never spend more than about 10 minutes above the local horizon.
  

• However, the orbital period of a spacecraft in a larger orbit will be longer. For an orbit of radius about 26,000 mi, the period will be 24 hours---the same as the rotation period of the Earth. Spacecraft here, if they are moving in the right direction, will appear to "hover" permanently over a given point on the Earth's surface. These orbits are therefore called geosynchronous or "geostationary." See the animation above. This is the ideal location for placing communications satellites.
  [The concept of geosynchronous communications satellites was first proposed by science fiction writer Arthur C. Clarke. He deliberately did not patent his idea, which became the basis of a trillion-dollar industry.]

Applications of Kepler's Third Law

Newton's theory verified Kepler's Third Law (described in Guide 7) and provided a physical interpretation of it. Newton found, as did Kepler, that for the planets in the Solar System, P² = K a³, where P is the period of a planet in its orbit, a is the semi-major axis of the orbit, and K is a constant. But his gravitational theory allowed him to show that the value of K is K = 4π²/GM, where M is the mass of the Sun.
More generally, K is inversely proportional to the mass of the primary body (i.e. the Sun in the case of the planetary orbits but the Earth in the case of orbiting spacecraft). The larger the mass of the primary, the shorter the period for a given orbital size.
• The Third Law therefore has an invaluable astrophysical application: once the value of the "G" constant has been determined (in the laboratory), the motions of orbiting objects can be used to determine the mass of the primary. This is true no matter how far from us the objects are (as long as the orbital motion and size can be measured).

• In the Solar System, the Third Law allows us to determine the mass of the Sun from the size and periods of the planetary orbits. It allows us to determine the mass of other planets from the orbits of their satellites. In the case of Jupiter, for example, the periods and sizes of the orbits of the Galilean satellites can be used to determine Jupiter's mass, as in Optional Lab 3.
  Remember that free-fall orbits are independent of the mass of the orbiting body. This means that the mass of a given planet cannot be determined from its motion or orbital size around the Sun.

• The Third Law was critical in determining the masses of other stars, using their orbits in binary star systems, and hence to deducing the physical processes that control stellar structure and evolution, one of the great accomplishments of 20th-century physics.

• The Third Law is applied today to such diverse astronomical problems as measuring the masses of "exoplanets" around other stars (see Study Guide 11) and establishing the existence of "Dark Matter" in distant galaxies.

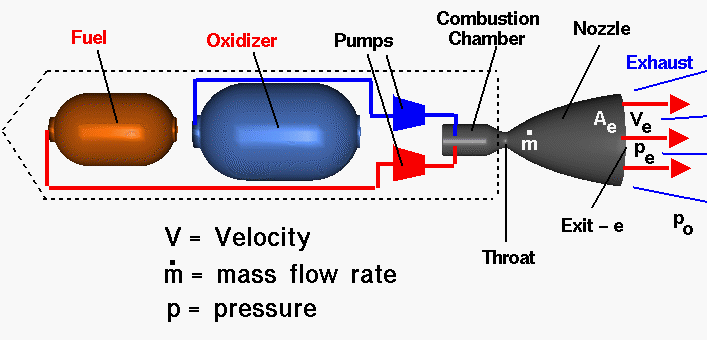
Schematic diagram of a liquid-fueled rocket engine. Rockets carry both fuel and an oxidizer,
which allows the fuel to burn even in the absence of an oxygen-rich atmosphere.
The thrust of the engine is proportional to the velocity of the exhaust gases (V_e).

C. Space Flight

If the primary technology enabling space flight is Newtonian orbit theory, the second most important technology is the rocket engine.

• In a rocket engine such as that shown in the diagram above, fuel combined with oxidizer is burned rapidly in a combustion chamber and converted into a large quantity of hot gas. The gas creates high pressure, which causes it to be expelled out a nozzle at very high velocity.
  The exhaust pressure simultaneously forces the body of the rocket forward. You can think of the rocket as "pushing off" from the moving molecules of exhaust gas. The higher the exhaust velocity, the higher the thrust.
  Note: rockets do not "push off" against the air or against the Earth's surface. Rather, it is the "reaction force" between the expelled exhaust and the rocket itself that impells the rocket forward.

  Designers work to achieve the highest possible exhaust velocity per gram of fuel. Newton's second law of motion and various elaborations of it are essential for understanding and designing rocket motors.
  [Rockets always carry their own supply of oxidizer (as seen in the diagram above). This distinguishes them from ordinary aircraft engines (propeller or "jet"), which use oxygen from the Earth's atmosphere as an oxidizer. Obviously, there aren't any handy oxidizers available in the vacuum of space.]

• The main challenge to spaceflight is obtaining the power needed to reach escape velocity. For Earth, this is 11 km/sec or 25,000 mph.
  The first successful launch of a spacecraft, the USSR's Sputnik-1, reached only 18,000 mph, but that was sufficient to place this "artificial satellite" into an elliptical orbit around Earth at several hundred miles altitude.
  Modern "standard" rocket engines are designed for launching commercial payloads to synchronous orbit or delivering intercontinental ballistic missles---neither of which involve reaching escape velocity from Earth. Therefore, most scientific spacecraft for planetary missions are relatively small (i.e. low mass) in order that standard engines can propel them past Earth escape velocity. This means that many clever strategies are needed to pack high performance into small, light packages.
  Example: The New Horizons spacecraft, launched on a super-high velocity trajectory to Pluto in 2006, has a mass of only 1050 lbs; its launching rocket weighed 1,260,000 lbs, over 1000 times more! New Horizons flew past Pluto in July 2015, traveling at over 34,000 mph, and has delivered a treasure-trove of images and other data on this most distant (3 billion miles from Earth at the encounter) of the classical planets.
  A rocket launched at exactly escape velocity from a given parent body will eventually, at very large distances, slow to exactly zero velocity with respect to that body (ignoring the effect of other gravitating bodies).

  The Apollo program used the extremely powerful Saturn V rockets to launch payloads with masses up to 100,000 pounds (including 3 crew members) to the Moon. This technology was, however, retired in the mid-1970's because it was thought, erroneously, that the next generation of "reusable" Space Shuttle vehicles would be cheaper to operate. A big mistake, because the reusable parts required extensive (and expensive) refurbishing for each new flight.
  The Space Shuttle (shown above) was fueled by high energy liquid oxygen and liquid hydrogen plus solid-rocket boosters. But it was so massive compared to the power of its engines that it could not reach escape velocity from Earth. Its maximum altitude is only about 300 miles. That is why NASA and the private sector are developing new "heavy lift" rocket technologies which have replaced the Shuttle, the most successful to date being the SpaceX Falcon and Dragon spacecraft.
  Modern rocket engines are remarkably complicated. Here is a simplified schematic of the Space Shuttle main engines.

D. Interplanetary Space Missions

Beginning in the early 1960's, NASA and foreign space agencies developed a series of ever-more sophisticated robot probes to study the Sun, Moon, planets, and the interplanetary medium. These included flyby spacecraft, orbiters, landers, rovers, and sample-return vehicles.

As of 2015, only 58 years after the first successful satellite launch (Sputnik, in 1957), we had flown at close range past every planet including Pluto; had placed robotic observatories into orbit around the Moon, Mercury, Venus, Mars, Jupiter, Saturn, three asteroids, and one comet; had sent probes into a comet nucleus and the atmosphere of Jupiter; had soft-landed on the Moon, Venus, Mars, Saturn's moon Titan, and the comet Churyumov-Gerasimenko; and had returned to Earth samples obtained from the coma of the comet Wild 2 and from a soft-landing on the asteroid Itokawa. And in 2013, the first human spacecraft left the Solar System altogether and entered interstellar space. At right is an artist's concept painting of the Cassini mission in orbit around Saturn.

We also put a number of highly capable remote-controlled observatories for studying the Solar System and the distant universe (such as the Hubble Space Telescope, the Chandra X-Ray Observatory, and the James Webb Space Telescope) into orbit around the Earth and the Sun.

Of course, the Apollo program in the 1960's also sent human beings to the Moon. But, by far, most of what we know about the denizens of the Solar System has come from our powerful robot missions and observatories, most of which were not even in development by the end of the Apollo program in 1972.

For a list of these missions and additional links, click here.

For a nice, prospective view of what human expansion over the next couple centuries into the deep space of our Solar System might look like, see this video, based on Carl Sagan's writings.

E. The Cost of Space Missions

Ever wonder why space flight is so expensive? It's because thousands of people are involved in almost any space endeavor, and it takes anywhere from 5 to 30 years to prepare a space mission.

Spacecraft require not only their own launching and maneuvering engines but also command and control systems, power supplies, thermal control, pointing and stabilization systems, protection from a harsh environment, sensors and scientific instruments, data taking and storage systems, communications systems, and more -- all of these subject to stringent weight and volume constraints -- plus extensive Earth-based infrastructure to monitor and operate them. All those people are required in order to design and build these myriad components and then certify that they will be at least 95% reliable after launch --- because, with very few exceptions, no repair is possible. They must identify and mitigate all possible failure modes. Reliability is the principal cost driver of space missions. Needless to say, because of the demands of human safety, the cost of crewed missions greatly exceeds that of comparably-scaled robot missions.

Two examples:

• Wikipedia reports that "The Gemini 9A mission (a 1966, 3-day, low Earth orbit test flight with two astronauts) was supported by 11,301 personnel, 92 aircraft and 15 ships from the U.S. Department of Defense" -- not to mention thousands of NASA and private sector personnel.

• The Apollo Moon program involved a total of 410,000 people and 20,000 companies. Its $150 billion budget (in 2019 dollars) supported about 1,200,000 person-years of effort over 10 elapsed years -- the largest non-military project in history. For a modern overview of the scope and complexity of the Apollo program, see the recent book "One Giant Leap" by Charles Fishman. NASA's overall budget history is shown here. At its peak, the Apollo program accounted for over 4% of the total US federal budget.

The overall unique scientific, commercial or exploratory value of a space mission must be weighed carefully against its projected cost.

To get a feel for the scale of effort involved in preparing and launching major spacecraft, watch this:

Apollo 11 Launch Video (ultra slo-mo, up-close-and-personal view of a Saturn V launch)
or this:
Shuttle Discovery Prep to Launch (remarkable time-lapse video)

The Hubble Space Telescope on orbit 300 miles above Earth

---

Reading for this lecture:

Bennett textbook: Ch. 4.1-4.4 (Newtonian dynamics & gravitational orbits)
Study Guide 8

Reading for next lecture:

Study Guide 9 (this material is not covered in the text)

---

Web links:

Recommended interactive sites illustrating orbits:
Newton's Mountain (Java animation), from Mike Fowler's UVa Physics course.
Gravity Chaos (Flash animation)--try to build multi-planet systems that don't self-destruct.

Orbits and Newton's Laws (Wikipedia)
Newton's Laws & Rockets. (Also see other pages on aeronautics at this site.)
JPL Notes on Basics of Space Flight
History of Space Flight (James Schombert, Univ. of Oregon)
Wade's Encyclopedia of Astronautics
Complete list of current, planned, and past NASA science missions
NASA/Johnson Space Center Digital Image Collection
Retrospective articles on 50 Years of the Space Race (New York Times)
The Apollo/Saturn V Moon rockets (the most powerful ever)
"Moon Machines - The Saturn V Rocket" documentary video
Introduction to UV and Space Astronomy (O'Connell)
The Astro/Ultraviolet Imaging Telescope Missions(O'Connell)
Lecture on space observatories (O'Connell)

---

Previous Guide

Guide Index

Next Guide

---

Last modified September 2023 by rwo

Text copyright © 1998-2023 Robert W. O'Connell. All rights reserved. Orbital animation copyright © Jim Swift, Northern Arizona University. Conic section drawings from ASTR 161, University of Tennessee at Knoxville. Newton's Mountain drawing copyright © Brooks/Cole-Thomson. These notes are intended for the private, noncommercial use of students enrolled in Astronomy 1210 at the University of Virginia.