IBETA

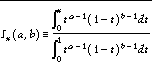
This routine is written in the IDL language. Its source code can be found in the file


ibeta.pro

in the

lib

subdirectory of the IDL distribution.

A positive integer, single-, or double-precision floating-point scalar that specifies the parametric exponent of the integrand.

A positive integer, single-, or double-precision floating-point scalar that specifies the parametric exponent of the integrand.

An integer, single-, or double-precision floating-point scalar, in the interval [0, 1], that specifies the upper limit of integration.

Compute the incomplete beta function for the corresponding elements of A, B, and X.

Define an array of parametric exponents.

A = [0.5, 0.5, 1.0, 5.0, 10.0, 20.0]

B = [0.5, 0.5, 0.5, 5.0, 5.0, 10.0]

Define the upper limits of integration.

X = [0.01, 0.1, 0.1, 0.5, 1.0, 0.8]

Allocate an array to store the results.

result = FLTARR(N_ELEMENTS(A))

Compute the incomplete beta functions. Note that the result for each element in the input arrays must be computed individually.

FOR K = 0, N_ELEMENTS(A)-1 DO $

result[K] = IBETA(A[K], B[K], X[K])

PRINT, result

IDL prints:

[0.0637686, 0.204833, 0.0513167, 0.500000, 1.00000, 0.950736]