 |
 |
The INT_3D function computes the triple integral of a trivariate function using iterated Gaussian quadrature. The algorithm's transformation data is provided in tabulated form with 15 decimal accuracy.
This routine is written in the IDL language. Its source code can be found in the file
int_3d.pro
in the
lib
subdirectory of the IDL distribution.
A scalar string specifying the name of a user-supplied IDL function that defines the trivariate function to be integrated. The function must accept X, Y, and Z, and return a scalar result.
For example, if we wish to integrate the following function:
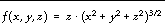
We define a function FXY to express this relationship in the IDL language:
A two-element vector containing the lower (A) and upper (B) limits of integration with respect to the variable x .
A scalar string specifying the name of a user-supplied IDL function that defines the lower (P( x )) and upper (Q( x )) limits of integration with respect to the variable y . The function must accept x and return a two-element vector result.
For example, we might write the following IDL function to represent the limits of integration with respect to y :
A scalar string specifying the name of a user-supplied IDL function that defines the lower (U( x,y )) and upper (V( x ,y)) limits of integration with respect to the variable z . The function must accept x and y and return a two-element vector result.
For example, we might write the following IDL function to represent the limits of integration with respect to z :
Compute the triple integral of the trivariate function
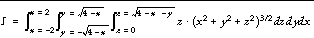
Using the functions and limits defined above, integrate with 10, 20, 48, and 96 point formulas (using double-precision arithmetic):
PRINT, INT_3D('Fxyz', [-2.0, 2.0], 'PQ_Limits', 'UV_Limits', 10, /D)
PRINT, INT_3D('Fxyz', [-2.0, 2.0], 'PQ_Limits', 'UV_Limits', 20, /D)
PRINT, INT_3D('Fxyz', [-2.0, 2.0], 'PQ_Limits', 'UV_Limits', 48, /D)
PRINT, INT_3D('Fxyz', [-2.0, 2.0], 'PQ_Limits', 'UV_Limits', 96, /D)
INT_3D with 10 transformation points yields: 57.444248
INT_3D with 20 transformation points yields: 57.446201
INT_3D with 48 transformation points yields: 57.446265
INT_2D , INT_TABULATED , QROMB , QROMO , QSIMP