 |
 |
The POWELL procedure minimizes a user-written function Func of two or more independent variables using the Powell method. POWELL does not require a user-supplied analytic gradient.
POWELL is based on the routine
powell
described in section 10.5 of
Numerical Recipes in C: The Art of Scientific Computing
(Second Edition), published by Cambridge University Press, and is used by permission.
On input, P is an n -element vector specifying the starting point. On output, it is replaced with the location of the minimum.
On input, Xi is an initial n by n element array whose columns contain the initial set of directions (usually the n unit vectors). On output, it is replaced with the then-current directions.
An input value specifying the fractional tolerance in the function value. Failure to decrease by more than Ftol in one iteration signals completeness. For single-precision computations, a value of 1.0 ¥ 10 -4 is recommended; for double-precision computations, a value of 1.0 ¥ 10 -8 is recommended.
On output, Fmin contains the value at the minimum-point P of the user-supplied function specified by Func .
A scalar string specifying the name of a user-supplied IDL function of two or more independent variables to be minimized. This function must accept a vector argument X and return a scalar result.
For example, suppose we wish to minimize the function
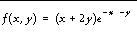
To evaluate this expression, we define an IDL function named POWFUNC:
We can use POWELL to minimize the function POWFUNC given above.
ftol = 1.0e-4 ; Define the fractional tolerance.
P = [.5d, -.25d] ; Define the starting point.
xi = TRANSPOSE([[1.0, 0.0],[0.0, 1.0]]) ; Define the starting directional vectors in column format.
POWELL, P, xi, ftol, fmin, 'powfunc' ; Minimize the function.
PRINT, P ; Print the solution point.
The exact solution point is [-0.31622777, -0.63245553].