 |
 |
The DFPMIN procedure minimizes a user-written function Func of two or more independent variables using the Broyden-Fletcher-Goldfarb-Shanno variant of the Davidon-Fletcher-Powell method, using its gradient as calculated by a user-written function Dfunc .
DFPMIN is based on the routine
dfpmin
described in section 10.7 of
Numerical Recipes in C: The Art of Scientific Computing
(Second Edition), published by Cambridge University Press, and is used by permission.
On input, X is an n -element vector specifying the starting point. On output, it is replaced with the location of the minimum.
On output, Fmin contains the value at the minimum-point X of the user-supplied function specified by Func .
A scalar string specifying the name of a user-supplied IDL function of two or more independent variables to be minimized. This function must accept a vector argument X and return a scalar result.
For example, suppose we wish to find the minimum value of the function
y = ( x 0 - 3) 4 + ( x 1 - 2) 2
To evaluate this expression, we define an IDL function named MINIMUM:
A scalar string specifying the name of a user-supplied IDL function that calculates the gradient of the function specified by Func . This function must accept a vector argument X and return a vector result.
For example, the gradient of the above function is defined by the partial derivatives:
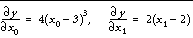
We can write a function GRAD to express these relationships in the IDL language:
Use this keyword to specify a number close to the machine precision. For single-precision calculations, the default value is 3.0 ¥ 10 -8 . For double-precision calculations, the default value is 3.0 ¥ 10 -16 .
Use this keyword to specify the maximum number of iterations allowed. The default value is 200.
To minimize the function MINIMUM (shown above):
X = [1.0, 1.0] ; Make an initial guess (the algorithm's starting point).
Gtol = 1.0e-7 ; Set the convergence requirement on the gradient.
DFPMIN, X, Gtol, Fmin, 'minimum', 'grad'