 |
 |
The FV_TEST function computes the F-statistic and the probability that two sample populations X and Y have significantly different variances. X and Y may be of different lengths. The result is a two-element vector containing the F-statistic and its significance. The significance is a value in the interval [0.0, 1.0]; a small value (0.05 or 0.01) indicates that X and Y have significantly different variances. This type of test is often referred to as the F-variance test.
The F-statistic formula for sample populations x and y with means ` x and ` y is defined as:
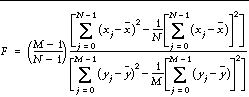
where x = ( x 0 , x 1 , x 2 , ..., x N-1 ) and y = ( y 0 , y 1 , y 2 ..., y M-1 )
This routine is written in the IDL language. Its source code can be found in the file
fv_test.pro
in the
lib
subdirectory of the IDL distribution.
Define two n-element sample populations.
X = [257, 208, 296, 324, 240, 246, 267, 311, 324, 323, 263, $
305, 270, 260, 251, 275, 288, 242, 304, 267]
Y = [201, 56, 185, 221, 165, 161, 182, 239, 278, 243, 197, $
271, 214, 216, 175, 192, 208, 150, 281, 196]
Compute the F-statistic (of X and Y) and its significance.
The result indicates that X and Y have significantly different variances.