 |
 |
The FX_ROOT function computes real and complex roots of a univariate nonlinear function using an optimal Müller's method.
This routine is written in the IDL language. Its source code can be found in the file
fx_root.pro
in the
lib
subdirectory of the IDL distribution.
A 3-element real or complex initial guess vector. Real initial guesses may result in real or complex roots. Complex initial guesses will result in complex roots.
A scalar string specifying the name of a user-supplied IDL function that defines the univariate nonlinear function. This function must accept the vector argument X.
For example, suppose we wish to find a root of the following function:
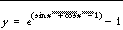
We write a function FUNC to express the function in the IDL language:
Use this keyword to specify the stopping criterion used to judge the accuracy of a computed root r( k ). Setting STOP = 0 (the default) checks whether the absolute value of the difference between two successively-computed roots, | r( k ) - r( k +1) | is less than the stopping tolerance TOL. Setting STOP = 1 checks whether the absolute value of the function FUNC at the current root, | FUNC(r( k )) |, is less than TOL.
To find the roots of the function FUNC defined above, first define a real 3-element initial guess vector:
Compute a root of the function using double-precision arithmetic.
root = FX_ROOT(X, 'FUNC', /DOUBLE)
Check the accuracy of the computed root.
PRINT, EXP(SIN(ROOT)^2 + COS(ROOT)^2 - 1) - 1
We can also define a complex 3-element initial guess vector:
X = [COMPLEX(-!PI/3, 0), COMPLEX(0, !PI), COMPLEX(0, -!PI/6)]
root = FX_ROOT(x, 'FUNC') ; Compute the root of the function.
Check the accuracy of the computed complex root.