 |
 |
The FZ_ROOTS function is used to find the roots of an m -degree complex polynomial, using Laguerre's method. The result is an m -element complex vector.
FZ_ROOTS is based on the routine
zroots
described in section 9.5 of
Numerical Recipes in C: The Art of Scientific Computing
(Second Edition), published by Cambridge University Press, and is used by permission.
EXAMPLE 1:" Real coefficients yielding real roots.
P ( x ) = 6 x 3 - 7 x 2 - 9 x - 2 (The exact roots are -1/2, -1/3, 2.0)
coeffs = [-2.0, -9.0, -7.0, 6.0]
( -0.500000, 0.00000)( -0.333333, 0.00000)( 2.00000, 0.00000)
EXAMPLE 2: Real coefficients yielding complex roots.
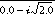 ,
, 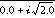 ,
,  ,
, 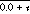
coeffs = [2.0, 0.0, 3.0, 0.0, 1.0]
(0.00000, -1.41421)(0.00000, 1.41421)
(0.00000, -1.00000)(0.00000, 1.00000)
EXAMPLE 3: Real and complex coefficients yielding real and complex roots.
P ( x ) = x 3 + (-4 - i 4) x 2 +s (-3 + i 4) x + (18 + i 24)
(The exact roots are -2.0, 3.0, (3.0 + i 4.0))
coeffs = [COMPLEX(18,24), COMPLEX(-3,4), COMPLEX(-4,-4), 1.0]
( -2.00000, 0.00000) ( 3.00000, 0.00000) ( 3.00000, 4.00000)