ASTR 1210 (O'Connell) Study Guide
7. THE DISCOVERY OF GRAVITY

Thomas Digges' version of the
Copernican Universe (1576)
A. Expanding Horizons
Copernicus' conception of a heliocentric universe sparked immediate controversy because it contradicted both the scientific and religious conventions of the times. It was hotly debated in the 150 years following publication of De revolutionibus, the most famous episode being the recantation of heliocentrism forced upon Galileo by the Catholic Church (1633). But a number of thinkers quickly and enthusiastically embraced the Copernican model, including Thomas Digges (d. 1595) in England and Giordano Bruno (d. 1600) in Italy. Even though Copernicus himself had pictured the stars as lying in a shell at a fixed distance from Earth, both Digges and Bruno realized that the model allowed the stars to be arbitrarily far away. In the first published description of heliocentrism in English, Digges drew the stars as stretching away to infinity (see the picture at the top of this page), and his inscription ( "This orb of stars fixed infinitely up extendeth itself in altitude spherically...with perpetual shining glorious lights innumerable...replenished with perfect endless joy...") shows that he was thrilled by this prospect. His concrete depiction of an infinite universe had lasting influence on later English scientists. Bruno emphasized the possibility that the stars were other Suns and that an unbounded universe was filled with inhabited planets orbiting other stars (a "plurality of worlds"):| "There are countless suns and countless earths all rotating round their suns in exactly the same way as the seven planets of our system. We see only the suns because they are the largest bodies and are luminous, but their planets remain invisible to us because they are smaller and non-luminous. The countless worlds in the universe are no worse and no less inhabited than our earth...The unnumbered worlds in the universe are all similar in form and rank and subject to the same forces and the same laws." |
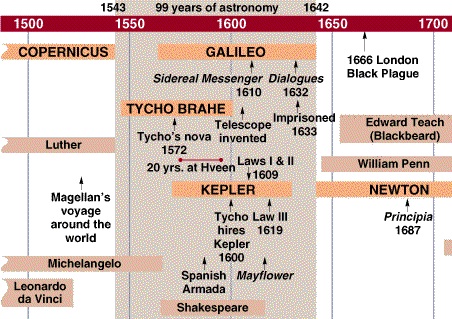
B. Tycho (d. 1601)

- Tycho uses a version of the parallax technique, based on observations taken 6-8 hours apart, to show that the supernova is more distant than Saturn and therefore must reside in the cosmic region the Greeks believed to be unchanging.
- Similarly, Tycho showed that the bright comet of 1577 lay beyond the Moon. Previously, it was assumed that comets (obviously changing from day to day) had to be phenomena inside Earth's atmosphere.
- The idea that there were changes in the distant cosmos other than the serene circular motions favored by astronomers up to this time was startling. Not only did this fatally damage the cozy medieval picture of a tranquil, eternal universe beyond Earth, but it obviously made the distant universe of much greater intellectual interest than it may have been before.
- Primary reason? Because he did not believe the stars could be so distant that he could not measure their parallaxes. This is a sound scientific argument and a major obstacle to earlier acceptance of the Copernican model.
- If Tycho could have measured stellar parallaxes, he would have instantly become a Copernican. But the distances between stars would have had to be about 100 times smaller than they are for that to be possible without telescopes. (Interestingly, that would have been the case had the Earth been situated in the central core of our Galaxy rather than in its outskirts.)
 Here is an animation of the
stellar parallax effect as it would be observed with a modern telescope.
Here is an animation of the
stellar parallax effect as it would be observed with a modern telescope.

Galileo's notes on the discovery of the satellites of Jupiter.
C. Galileo (d. 1642)

-
Galileo gave experiment and observation explicit precedence over
authority. (Recall the discussion of the role of authority in
modern science in Guide 1.) His many
amazing discoveries made with small telescopes were a resounding
demonstration of the superiority of empiricism in learning
about nature. His disdain for a reliance on authority and his
devotion to mathematical empiricism are often expressed in his
writings:
| "You must read the book of Nature... In other words, observe and do experiments. This is against the medieval idea of scholasticism--that all wisdom and knowledge are best found in ancient authorities." "Truth cannot be found in the book of Aristotle but in the book of Nature; and the book of Nature is written in the language of mathematics." "...without [mathematics] we are wandering in vain through a dark labyrinth." |
- Experimentally, he demonstrates that objects falling in
response to gravity accelerate---that is, increase
their velocity---in a highly systematic way (directly proportional to
time) and that their acceleration is independent of their
mass.
-
Among other things, this means that two objects if dropped
simultaneously from any height will hit the ground at the same time
(ignoring extraneous effects like atmospheric drag) no matter how much
they differ in mass.
- He realizes that these results, and those of many other of his
experiments, flatly contradict the principles of Aristotlean
physics. Aristotle had naively assumed, as do most people, that
heavier objects fall faster than lighter ones and that downward
velocities are constant. Owing to the Greek distrust of experiment,
Aristotle's assumptions had not been subjected to empirical tests, nor
had most of the other details of
his writings
on physics.
-
Isn't it amazing that you, if you did
the "object drop"
assignment in Guide 6, were able to make a very simple experiment
in your dorm room that invalidates the claims of one of the most
famous philosophers in history and that were assumed for be true for
1900 years? That's the power of empirical exploration of the real
world.
At least one Greek scientist, Strato, was aware of gravitational
acceleration: he had observed the increasing separation between
water droplets as they fall from a spout. But as in the case
of Aristarchus, this important insight was submerged by the
overwhelming influence of Aristotle on later thinking.
- Galileo made the first astronomical use of a
telescope in 1609. He had learned of the invention of telescopes
by Lippershey
in Holland and quickly decided to make his own.

One of Galileo's telescopes. (Click for details.) 
Galileo demonstrating telescope to his patrons - Galileo's telescopes were small (above), with relatively crude
lenses only a few inches in diameter. But they yielded the first
fundamentally new observational insights in over 1500 years.
They utterly transformed astronomy. They allowed Galileo to
discover:
- Mountains and craters on the Moon.
- That spots first observed by others on the Sun were features on the solar surface (not intervening material, for instance) and showed that the Sun rotated on an axis.
- The existence of thousands of stars fainter than the eye can see. The "Milky Way" was revealed to be made up of a myriad of stars.
- That stars and planets are different kinds of objects: planets show perceptible disks, but stars are points of light, which implies they are probably very far away.
- Four satellites in orbit around Jupiter (now named the "Galilean satellites"). These were the first new planetary bodies discovered in recorded history. They are the four brightest of the (now known) 92 satellites of the planet.
- The phases of Venus
- Galileo was so amazed and delighted by his new discoveries that he rushed to publish them in Sidereus Nuncius ("The Celestial Messenger"), one of the most important books in the history of science and an immediate bestseller.
- Galileo's telescopes were small (above), with relatively crude
lenses only a few inches in diameter. But they yielded the first
fundamentally new observational insights in over 1500 years.
They utterly transformed astronomy. They allowed Galileo to
discover:
- These discoveries strongly support the Copernican interpretation,
though they don't actually prove it:
- The craters on the Moon and spots on the Sun contradict the claims of the Greeks and the Catholic Church about the perfection of the heavenly bodies, which then cast doubt on their other pronouncements.
- The rotation of the Sun demonstrates that celestial bodies can spin, which supports Copernicus' assumption that the Earth spins on its axis.
- Copernicus' assumption that the Earth is a planet meant that the other planets should share some of Earth's characteristics: they should be round, they should shine by reflected Sunlight, and they should show surface features. All of these "predictions" were verified by Galileo's observations.
- The fact that Venus displays an almost full range of phases from "crescent" to nearly "full" proves that Venus orbits the Sun, not the Earth. In Ptolemy's model, the epicycles of both Mercury and Venus lie between Earth and the Sun, so Venus can never appear in other than a crescent phase. See this illustration of the difference between the Copernican and Ptolemaic interpretation.
- Jupiter's satellites show the existence of a second "center of motion" in the solar system. This ruins the acclaimed symmetry of the geocentric model, in which the Earth lies at the only center of motion in the universe. Galileo's observations also showed that planets can move without "losing" their satellites. It had been argued that if the Earth moved around the Sun, the Moon would be left behind. Not so.
- In another blow to conventional wisdom, the discovery of vast numbers of previously invisible stars shows that the stars are not simply some kind of celestial decoration, "put there" for the benefit or instruction of human beings. This is the first evidence of a huge physical system of stars surrounding the Sun, confirming the speculations of Digges and Bruno, and the most important contribution to that time to the argument that the Sun itself is a star.
- The telescope is sufficiently cheap and easy to build
that anyone can test claims made about the nature of
astronomical objects. The availability of printed books and simple
instruments like telescopes encouraged the questioning of traditional
authorities, somewhat like the Internet in our time.
- The subsequent history of astronomy was revolutionized at intervals by the advent of new telescope designs and auxiliary equipment.
D. Kepler (d. 1630)

- Because of his great respect for Tycho's precise observational technique, Kepler insisted that interpretive models agree with the observations within observational uncertainty or "error." Where there is a disagreement, it is the model, not the data, that must be revised. Empirical data takes precedence.
- This is the basis of modern empiricism. Today, this requirement for acceptable interpretations is taken to extend to all relevant data. It is a demand for consistency with all interpreted phenomena and established physical principles. This is the "cumulative" aspect of science described in Study Guide 1.
- The term "error" used in this context does not imply some kind of mistake. Instead, it refers to the uncertainties that are inherent in any measuring process, no matter how careful. An essential part of a scientist's job is always to make good estimates of the uncertainty in any published data.
- He works eight years to resolve an 8 arc-min discrepancy between the models and data. (The discrepancy was 8 times the observational uncertainty of Tycho's data.)
- He finally realizes that Mars' orbit is an ellipse, not a
circle
-
Ellipses are perfectly well-defined geometrical figures, first studied
by the ancient Greek mathematicians. But because they are less
symmetrical than circles, Ptolemy did not attempt to incorporate them
in his cosmological model.
Other than Mercury, Mars has the most eccentric (non-circular) orbit
of the five planets then known -- but Mercury is harder to observe and
had less extensive coverage in Tycho's data sets. That is why the
data for Mars was critical to Kepler's discoveries.
- The methods Kepler used to achieve this breakthrough are re-created in the ASTR 1210 optional laboratory on the Orbit of Mars.
Kepler's Laws
- Planetary orbits are ellipses with the Sun at one focus
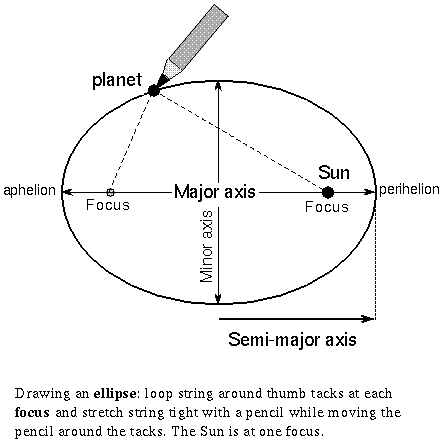
- Note that the Sun is not at the center of the ellipse and that there is nothing there or at the second focus of the orbital ellipse. The distance between any planet and the Sun will vary as it moves around its orbit.
- The Sun is in the same plane as the ellipse for a given
planet, but the orbits of different planets can lie in different
planes.
-
The fact that the planes of the orbits of the other planets always
include the Sun but do not include the Earth is a simple but important
objection to geocentric interpretations of the Solar System.
- The planetary orbits are not very elliptical, which is why circles are fair approximations, as in Copernicus' model.
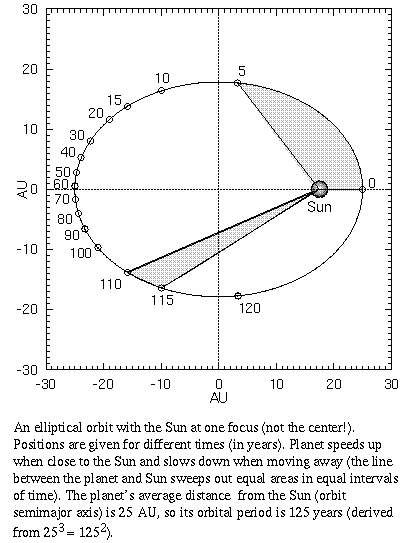
- For a given planet, a line joining the planet as it moves and the
Sun sweeps out equal areas in the orbital plane in equal times.
 Kepler's Second Law -- Click for
animation.
Kepler's Second Law -- Click for
animation. -
This implies a given planet moves faster when it is nearer the
Sun, with a specific (inverse) relationship between its sideways
motion and its distance.
[This behavior is also the first hint of a universal physical principle
not recognized until after Newton:
the conservation of angular momentum.]
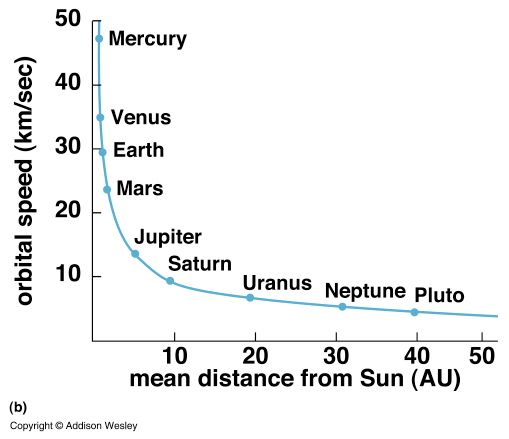
- The squares of the orbital periods of different planets are
proportional to the cubes of the orbital sizes (semi-major
axes -- see the illustration of Kepler's First Law
above).
-
In equation form, P2 = K a3, where P is
the period, a is the semi-major axis, and K is a constant.
The time P taken to complete one orbit is therefore proportional to (a x
a1/2) and grows more than in direct
proportion to orbital size.
-
A planet with an orbital diameter 5 times the Earth's will
require 11 Earth years to complete an orbit.
-
A planet's mean velocity in its orbit is equal to the circumference
of the orbit divided by its orbital period. Since the circumference
of an orbit increases in direct proportion to its semi-major axis, but
the period increases more than in direct proportion, the mean
velocity of planets in larger orbits is slower. See graph above right.
-
The complexities such as epicycles in Ptolemy's model were
needed because of three principal factors: the fact that the
Earth moves, whereas Ptolemy assumed it to be stationary; the fact
that actual orbits are elliptical, whereas he assumed them to be
circular; and the fact that the velocity of a planet in its orbit
varies, whereas he assumed constant circular velocities.
Kepler's laws and the concept of force
- In the early Greek cosmologies, there was no need for a special "force" to control the motions of planets in their orbits, since all the cosmic bodies were thought to be affixed to crystalline spheres, and the tendency of things to fall downward was thought to be the product of Earth's special location at the center of the universe, not something caused by the Earth itself.
- But in the real world revealed by Kepler's work, there are no crystalline spheres; rather, the Sun is the key to the planetary motions. It is not just the center of the solar system but is also directly linked to the geometry of planetary orbits and to motions within those orbits by precise but non-intuitive mathematical relations. Kepler therefore postulated that the Sun exerts a force on the planets---e.g. one which either pulls or pushes planets along their orbits. Another kind of force was thought to be required in order to keep the Moon and the satellites of Jupiter bound to their parent planets as they moved around the Sun. Although Kepler was unable to formulate this idea properly, Newton did so with phenomenal success.
Kepler's laws and the speed of light
- Within 100 years, an avalanche of observations had shown that planetary motions obey Kepler's laws with remarkable precision. The laws were even extended to the motion of the four Galilean moons in orbit around Jupiter. The laws allowed astronomers to predict the eclipses of the moons by the body of Jupiter. However, measurements over about a decade showed that there were worrisome systematic discrepancies from the predicted Keplerian timing of eclipses. These were not understood, but it did emerge that they depended on the Earth's distance from Jupiter (which, due to their relative orbital sizes, varies from 4 to 6.5 AU's).
- In 1676 Danish astronomer Ole Romer, shown observing at the right, interpreted the discrepancies as the consequence of a finite value for the speed of light: light took longer to reach the Earth from Jupiter when the two planets were farther apart and delayed the times of the expected eclipses. Allowing for this delay confirmed the predictions from Kepler's Laws. This was the first evidence that light has a finite propagation speed. Romer's estimated value for the speed of light was about 25% smaller than modern determinations, but this was an extraordinary achievement for his time.

E. Newton (d. 1727)

-
Newton's First Law of Motion
- In the absence of a (net) force, an object will remain at rest or in straight-line motion with no change in velocity.
- The presence of a net force produces a change in velocity (i.e. an acceleration).
- This law directly contradicts Aristotle, who believed that objects cannot move at all unless subjected to a continuous force. Newton argues that continuous, uniform motion only occurs in the absence of a force.
- The quantitative relationship between applied force and resulting
acceleration is
-
(Force) = (Mass) x (Acceleration)
Or, solving for the acceleration: (Acceleration) = (Force)/(Mass)
There is a directionality inherent in this formulation. Mass has
no "direction," but forces do. The Second Law implies that the acceleration
will occur in the same direction as the applied force.
- The second law is covered in more detail in Guide 8 and in the Supplements.
- Kepler had introduced the idea of a special force, exerted by the Sun on the planets to keep them moving in their elliptical orbits. Newton brilliantly adapted this concept, realizing that all bodies could exert a force on one another. In particular, the Earth could exert a force on the Moon to keep it in its orbit around the Earth. But in that case the Earth should also exert a force on objects near the Earth's surface.
- Newton argued that our everday experience of "gravity" (our sense of a downward pull or the downward acceleration of falling objects) was a manifestation of exactly the same kind of force, exerted by the Earth, that kept the Moon in its orbit. He sought a formulation that would simultaneously explain local gravity and planetary orbits.
- So Newton postulated the existence of a universal
gravitational force in the following form:
Every object with mass exerts an attractive force on every
other object with mass, and the force declines with distance.
Quantitatively:
-
Fgrav = G M1 M2 / R2
where G is a universal constant, the M's are the masses of the two
objects, and R is the distance between the two masses
The same expression applies to the Earth's influence on a falling
apple, to the Earth's influence on the Moon, to the Sun's influence on
the Earth, and so on.
The gravitational force diminishes rapidly with distance.
Quantitatively, it is an "inverse square law," with the
force declining as the square of the distance between the two
masses. The Sun's gravitational force on two identical planets,
one of which is 1 AU from the Sun and the other of which is 5 AU
distant would differ by a factor of 52 or 25.
Importantly, however, the force only becomes very small with
distance, it never actually vanishes (or goes to zero). So,
all the stars in our Galaxy, for example, combine gravitationally
to determine the motion of the Sun around the Galaxy, despite their
being, on average, tens of thousands of light years away.
Also, by its formulation, the strength of the gravitational force
is the same on both masses and differs only in direction.
Both masses will move in response to the force -- but the
motion is inversely proportional to mass, so the smaller
mass moves faster (see Guide 8).
- Gravity acts along the (radial) line connecting the two bodies. It therefore does not (as Kepler thought) necessarily act to "push" or "pull" objects along their current directions of motion. In fact, for a circular orbit, the gravitational force acts perpendicular to the direction of motion. Although this sounds paradoxical, it has a simple explanation in the context of Newtonian dynamics, which we explain in Study Guide 8.
- Newton's formulation of gravity would have been conceptually
impossible without the elimination by Copernicus of the assumption of
the special, central location of the Earth.
-
And conversely, the geocentric, circular-motion universe becomes
impossible if one accepts the reality of Newtonian gravity.
- [Modern footnote: Gravity was only the first universal force to be recognized. Physics now recognizes four types of force, the other three all much stronger than gravity but having much shorter ranges in practice. See Supplements 2 & 3.]

- Newton combined his gravitational force law with his Second Law of motion in order to predict the motion of an object in an external gravitational field. To solve the equations, Newton had to invent calculus.
- For two gravitating objects (e.g. one planet and the Sun) the predicted orbit satisfies all three of Kepler's Laws. Details are given in Study Guide 8.
- Newton's theory explained all the known properties of the
planetary orbits and also the motion of objects (like apples, bullets,
and pendulums) moving in Earth's gravity.
-
Remarkably, it was quickly extended to determine the orbit
of Halley's Comet
(which was correctly predicted
to return in
1759) and to explain the ocean tides, the
Earth's precession, the Earth's
oblate shape, and many other formerly mysterious phenomena.
- In 1846 Newton's theory was used to correctly predict the location of a new planet, Neptune, based on unexpected residuals in the orbit of the planet Uranus. This was regarded as the "greatest triumph" of Newtonian mechanics.
-
Newton's Laws and theory of gravity were complete, quantitative,
and predictive. They were profoundly clarifying, and their
importance extended vastly beyond their original frame of reference.
They represent the first generalized physical laws. From them emerged
modern physics, mathematics, and engineering. They became the
cornerstone of the "Scientific Revolution."
Reading for this lecture:
-
Bennett textbook: Ch. 3.3 (Copernicus, Tycho, Kepler, Galileo)
Study Guide 7
Further optional reading: Arthur Koestler, The Sleepwalkers; Timothy
Ferris, Coming of Age in the Milky Way; J. L. E. Dreyer,
A History of Astronomy from Thales to Kepler; Richard
S. Westfall, Never at Rest: A Biography of Isaac Newton.
-
Bennett textbook: Ch. 4.1, 4.2, 4.3, 4.4 (Newtonian dynamics & gravitational orbits)
Study Guide 8
Web links:
-
Slides
shown in lecture
The Path to Newton
(Summarizes in text and graphical form the key conceptual
developments leading to Newton's laws of motion and gravity) More information on Tycho
Images of Tycho (Oxford University exhibition) The Galileo Project. (elaborate site devoted to Galileo and his times)
The Trial of Galileo (the most famous collision between science and religion)
Galileo's Moon (an episode of the PBS TV series "Secrets of the Dead" concerning the impact of Sidereus Nuncius) More information on telescopes (Study Guide 14) Biography of Kepler (Mike Fowler, PHYS 109)
Biography of Kepler (MacTutor Archive)
More information on Kepler's Laws (Wikipedia)
Kepler's Discovery (background on Kepler and his science) Flashlet Interactive Simulation of Kepler's Laws (Mike Fowler)
Java Simulation of Solar System Orbits Shows shapes and orbital speeds. (UMd)
Java Simulation of Parallax (UBC) The Newton Project (Oxford University)
Biography and Contributions of Newton, with many supporting links (Weisstein)
Voltaire's comments on Newton (at a distance of 100 years)
More information on Newton's Laws (Study Guide 10/Supplements II and III)
JPL Notes on Gravitation & Mechanics (Kepler's & Newton's laws & applications to spaceflight)
 Previous Guide
Previous Guide
|
 Guide Index
Guide Index
|
 Next Guide
Next Guide
|