ASTR 1210 (O'Connell) Study Guide
8. GRAVITATIONAL ORBITS AND SPACE FLIGHT

Space Shuttle Discovery launches on
a mission
to the Space Station, 2001
|
"There will certainly be no lack of human pioneers when we have
mastered the art of [space] flight....Let us create vessels and sails adjusted
to the heavenly ether, and there will be plenty of people unafraid of
the empty wastes. In the meantime we shall prepare, for the brave
sky-travelers, maps of the celestial bodies." |
A. Newtonian Orbit Theory
Orbital Dynamics
Newton's theory can accurately predict gravitational orbits because it allows us to determine the acceleration of an object in a gravitational field.-
Acceleration is the rate of change
of an object's velocity.
If we know the
initial position and velocity of an object, knowing its acceleration
at all later times is enough to completely determine its later path of
motion.
To predict the path, we simply substitute Newton's expression
for Fgrav for the force term in his
Second
Law and solve for acceleration:
-
a = Fgrav/m
But there are major complications. The Second Law is not a simple
algebraic expression. Both velocity and acceleration are rates of
change (of position and velocity, respectively). Mathematically,
they are derivatives. The gravitational force also changes with
position. Finally, velocity, acceleration and the gravitational force
all have a
directionality as well as a magnitude associated with
them. That is, they are "vectors".
So the Second Law is really a differential vector
equation. To solve it, Newton had to
invent
calculus.
-
Pick any location on the Earth's orbit. Represent its velocity at that
location as an arrow (a vector) showing the direction and magnitude
of its motion.
An essential element of Newtonian theory is that changes in
the magnitude of the velocity vector (the speed) or in
the direction of motion are both considered to be
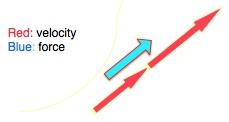
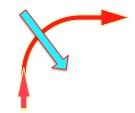
"accelerations." In the following drawings, the red arrows represent
the Earth's velocity vector and the blue arrows represent the applied
gravitational force. According to Newton's Second Law, the change
in the velocity vector (a speed-up in the first case or a
deflection of the direction of motion in the second) is in the
direction of the applied force.
|
|
 You might think that if the acceleration is always toward the Sun,
then the Earth should fall faster and faster on a radial trajectory
until it crashes into the Sun. That's exactly what would
happen if the Earth were ever stationary in its orbit.
In that case, the situation in the left hand drawing above (straight-line
acceleration toward the Sun) would prevail.
But if the Earth's velocity vector has a component which is perpendicular
to the radial direction, then in any interval in time, it will move
"sideways" at the same time as it accelerates toward the Sun.
If the combination of sideways motion and distance from the Sun is
correct, the Earth will avoid collision with the Sun, and it will
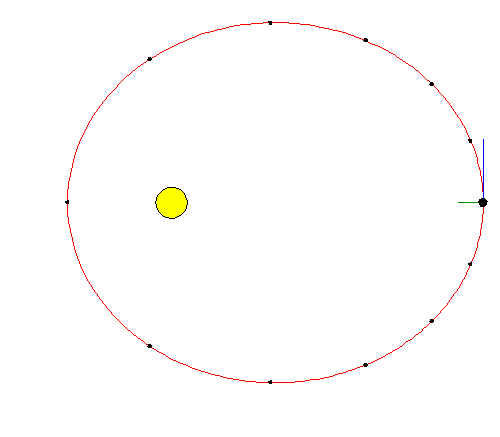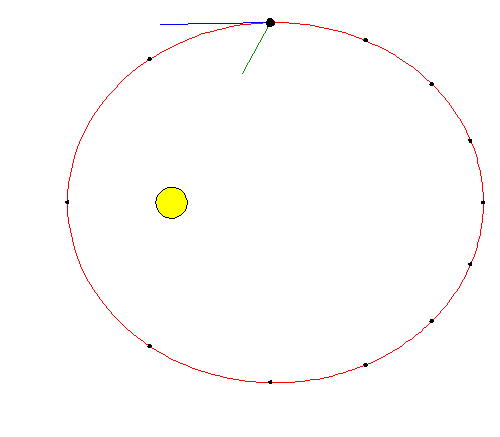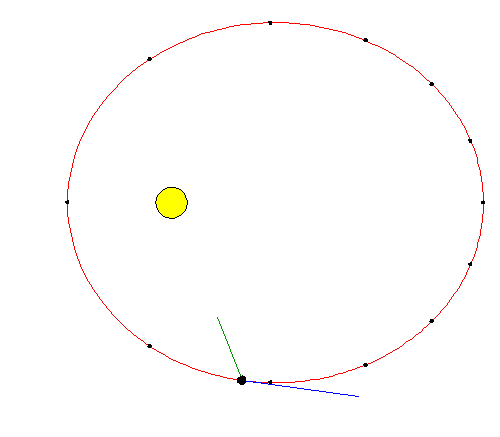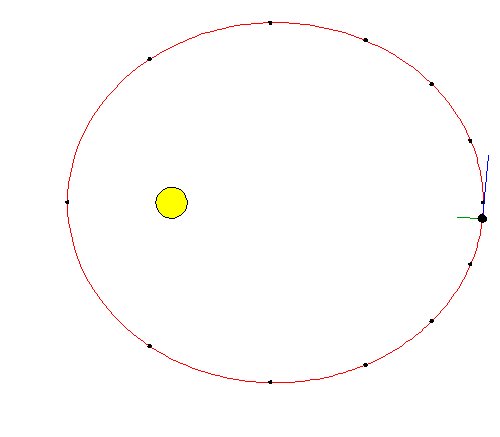
stay in permanent orbit. The animation at the right shows the
situation for the Earth's (exaggerated) elliptical orbit around the
Sun (here, the blue line is the velocity vector, the green line is the
acceleration;
click for an
enlargement). Note that where
the Earth is nearest the Sun, the gravitational force and inward acceleration
are greatest, but the sideways motion is also greatest, which prevents us
from colliding with the Sun. That motion is in accordance with
Kepler's
second law.
Therefore, all permanently orbiting bodies are perpetually
falling toward the source of gravity but have enough sideways
motion to avoid a collision.
You might think that if the acceleration is always toward the Sun,
then the Earth should fall faster and faster on a radial trajectory
until it crashes into the Sun. That's exactly what would
happen if the Earth were ever stationary in its orbit.
In that case, the situation in the left hand drawing above (straight-line
acceleration toward the Sun) would prevail.
But if the Earth's velocity vector has a component which is perpendicular
to the radial direction, then in any interval in time, it will move
"sideways" at the same time as it accelerates toward the Sun.
If the combination of sideways motion and distance from the Sun is
correct, the Earth will avoid collision with the Sun, and it will
stay in permanent orbit. The animation at the right shows the
situation for the Earth's (exaggerated) elliptical orbit around the
Sun (here, the blue line is the velocity vector, the green line is the
acceleration;
click for an
enlargement). Note that where
the Earth is nearest the Sun, the gravitational force and inward acceleration
are greatest, but the sideways motion is also greatest, which prevents us
from colliding with the Sun. That motion is in accordance with
Kepler's
second law.
Therefore, all permanently orbiting bodies are perpetually
falling toward the source of gravity but have enough sideways
motion to avoid a collision.
Kinds of Gravitational Orbits
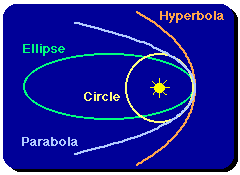
In the case of two gravitating objects (for example, the Earth and the Moon, the Sun and a planet, or the Earth and an artificial satellite), Newton found that the full solutions of his equations give the following results: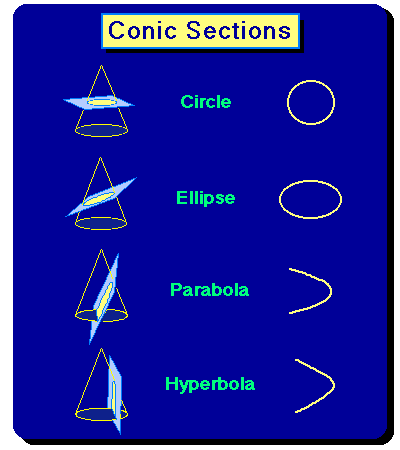
- The relative orbit is confined to a geometric plane which contains both objects.
- The shape of the orbit within the plane is a "conic section",
of which there are only four types.
- A circle
- An ellipse
- A parabola
- A hyperbola See the illustration at the right.
- A circle
- The orbital type is determined by the
initial distance, speed (V) and
direction of motion of the orbiting object, as follows:
- Define the "escape velocity" at a given
distance: Vesc(R) = √(2GM/R), where R
is the separation between the two objects and M is
the mass of the primary object.
-
Vesc for the Earth at the Earth's surface is 25,000 mph (or 11 km/s).
Vesc for the Sun at the Earth's 1 AU distance from the Sun
is 94,000 mph (42 km/s).
- Define the "escape velocity" at a given
distance: Vesc(R) = √(2GM/R), where R
is the separation between the two objects and M is
the mass of the primary object.
- If V < Vesc, the orbit is an ellipse or circle. It is said to be "closed" or "bound". The smaller object will permanently repeat its orbital motion.
- If V ≥ Vesc, the orbit is a parabola or hyperbola. It is said to be "open" or "unbound". The smaller object escapes and does not return.
- Only specific values of velocity will yield circular or parabolic orbits. An object moving exactly at escape velocity will move on a parabola. To achieve a circular orbit an object must move at 71% of the escape velocity, and its velocity must be exactly perpendicular to the radial direction. Other combinations of velocity or direction lead to elliptical or hyperbolic orbits.
- As noted earlier, shapes and motions within the "closed" orbits for the planets satisfy all three of Kepler's Laws of planetary motion.
Newton's Mountain
Newton illustrated orbital behavior for a simple idealized situation where a powerful cannon is fixed in position on top of a high mountain on the Earth's equator. It is allowed to fire only with its barrel parallel to the Earth's surface (see the illustration below). Since both the distance from Earth's center and the direction of initial flight are fixed, the cannonball follows an orbit that depends only on the muzzle velocity of the cannon as shown below.-
The gravitational force of a spherical body like the Earth acts as
though it originates from the center of the sphere, so
elliptical orbits of the cannonball will have the center of the Earth
at one focus. The center of the Earth lies directly under the red
dot in the picture below.
(For simplicity, the diagram omits showing "orbits" where the muzzle
velocity is far enough below the circular orbit velocity that the
cannonball hits the surface of the Earth. Needless to say, that is
the situation for all real-life cannons; but the flight paths taken
before the collision do have elliptical shapes.)
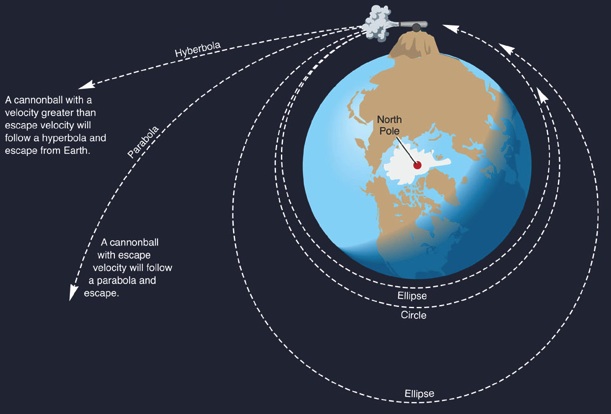
"Newton's Mountain": orbit type depends on
initial velocity.
From lower to higher velocities, orbit shapes are:
ellipse, circle, ellipse, parabola, hyperbola.
"Escape velocity" (which
is 25,000 mph at Earth's surface) produces
a parabolic orbit.
General Relativity
Much later (1915), Newton's theory was shown by Albert Einstein to be inadequate in the presence of large masses or over large distances and has been replaced by the General Theory of Relativity in such situations. Relativity theory profoundly changed our understanding of space and time, for example by demonstrating that mass and energy can affect the structure of space and time, something that Newton never contemplated. It is much more complicated mathematically than Newton's formulation. But as a practical matter, Newton's theory is an entirely satisfactory description of "everyday" gravity. Only very minor corrections to the Newtonian predictions are necessary, for example, to send spacecraft with high accuracy throughout the solar system.-
General Relativity predicted important phenomena that were not foreseen in
Newtonian physics,
including black
holes (closed regions of space-time around massive, compact
objects)
and
gravitational waves (propagating disturbances in the structure of
space-time).
The first detection of cosmic gravitational waves, generated by the
merger of two very distant black holes, was announced by
LIGO (the Laser
Interferometer Gravitational-Wave Observatory) in February of 2016.
This was one of the most difficult scientific experiments ever
attempted as well as a brilliant confirmation of the validity
of General Relativity.
B. Important Implications of Newtonian Orbits
"Free-Fall" Orbits
-
Free motion in response to gravity (in the absence of other forces) is
called "free-fall" motion. Conic section
orbits are all "free-fall orbits."
-
Remember that motion is normal in free-fall. For instance,
rocket engines do not have to be on in order for spacecraft to
move through space on a free-fall orbit. Spacecraft will "coast" forever on
such an orbit, just as do the planets in orbit around the Sun.
Note also that free-fall orbits will depart from simple conic
sections if an object is under the influence of
more than one gravitating body. For instance, comets
are often deflected from their Sun-dominated simple conic orbits by
Jupiter's gravity (see Guide 21),
and spacecraft traveling between the Earth and the Moon will not
follow simple conic paths.
-
Another way of stating this is to say that the acceleration of all
objects is the same in a given gravity field (e.g. at a given
distance from the Sun or near the Earth's surface), regardless of
their masses. This was first demonstrated experimentally
by Galileo
and was the subject of our "object drop" Puzzlah (see
Study Guide 7).
The mass of the orbiting body always
cancels out of the expression for acceleration under gravity.
For instance, in the case of a planet orbiting the Sun, the
gravitational force on the planet is directly proportional to
the planet's mass; but, according to Newton's Second Law, the resulting
acceleration is inversely proportional to its mass. So,
mass drops out of the expression for acceleration.
This is true for all orbits under gravity. Hence, a tennis ball in
space, if it were moving with the same speed and direction as the
Earth at any point, would follow exactly the same orbital path as the
Earth around the Sun.
Kepler's Third Law (that the orbital period of a planet around the Sun
depends only on its orbital size, not on the mass of the planet) is another
manifestation of this fact.
 A more familiar manifestation of "free fall" these days is the
phenomenon of "floating" astronauts on space missions. Even
though the spacecraft is much more massive, both the astronauts
and the spacecraft have identical accelerations under the
external gravitational fields. They are moving on parallel
free-fall orbits, so the astronauts appear to be floating and
stationary with respect to the spacecraft, even though they are
actually both moving at over ten thousand miles per hour in
near-Earth orbit.
A more familiar manifestation of "free fall" these days is the
phenomenon of "floating" astronauts on space missions. Even
though the spacecraft is much more massive, both the astronauts
and the spacecraft have identical accelerations under the
external gravitational fields. They are moving on parallel
free-fall orbits, so the astronauts appear to be floating and
stationary with respect to the spacecraft, even though they are
actually both moving at over ten thousand miles per hour in
near-Earth orbit.
 Here are some brief videos of free-fall on the Space
Shuttle during the Astro-2
UV observatory mission in 1995:
camera toss;
dinner flip;
tortilla catch.
Here are some brief videos of free-fall on the Space
Shuttle during the Astro-2
UV observatory mission in 1995:
camera toss;
dinner flip;
tortilla catch.
-
With its engine turned off, the motion of any
spacecraft is a free-fall orbit.
If the engine is on, the craft is
not in free fall. For instance, the orbit of the Space Shuttle
launching from the Earth will depart from a conic section until its
engines turn off. An example of using a rocket engine to change from
one free-fall orbit to another
is shown here.

The Russian "Mir" space station (1986-2001) orbiting Earth in free-fall at an altitude of 200 miles with a velocity of 17,000 mph
Geosynchronous Orbits
-
According to Kepler's Third Law, the
orbital period of a satellite will
increase as its orbital size increases. We have exploited that
fact in developing one of the most important practical
applications of space technology: geosynchronous satellites.
- Spacecraft in "low" Earth orbits (less than about 500 mi),
like the Mir space station (seen above) or the Space Shuttle, all
orbit Earth in about 90 minutes, at 17,000 miles per hour,
regardless of their mass. As seen from a given point on Earth's
surface, they travel quickly across the sky and never spend more
than about 10 minutes above the local horizon.

- However, the orbital period of a spacecraft in a larger orbit will be longer. For an orbit of radius about 26,000 mi, the period will be 24 hours---the same as the rotation period of the Earth. Spacecraft here, if they are moving in the right direction, will appear to "hover" permanently over a given point on the Earth's surface. These orbits are therefore called geosynchronous or "geostationary." See the animation above. This is the ideal location for placing communications satellites. [The concept of geosynchronous communications satellites was first proposed by science fiction writer Arthur C. Clarke. He deliberately did not patent his idea, which became the basis of a trillion-dollar industry.]
Applications of Kepler's Third Law
-
Newton's theory verified Kepler's
Third Law (described in Guide 7) and provided a physical
interpretation of it. Newton found, as did Kepler, that for the
planets in the Solar System, P2 = K a3,
where P is the period of a planet in its orbit, a is
the semi-major axis of the orbit, and K is a constant. But his
gravitational theory allowed him to show that the value of K is K =
4π2/GM, where M is the mass of the Sun.
More generally, K is inversely proportional to the mass of the
primary body (i.e. the Sun in the case of the planetary orbits but
the Earth in the case of orbiting spacecraft). The larger the
mass of the primary, the shorter the period for a given
orbital size.
- The Third Law therefore has an invaluable astrophysical application: once the value of the "G" constant has been determined (in the laboratory), the motions of orbiting objects can be used to determine the mass of the primary. This is true no matter how far from us the objects are (as long as the orbital motion and size can be measured).
- In the Solar System, the Third Law allows us to determine the
mass of the Sun from the size and periods of the planetary orbits.
It allows us to determine the mass of other planets from the
orbits of their satellites. In the case of Jupiter, for example, the
periods and sizes of the orbits of the Galilean satellites can be used
to determine Jupiter's mass, as
in Optional Lab 3.
-
Remember that free-fall orbits are independent
of the mass of the orbiting body. This means that the mass of a given
planet cannot be determined from its motion or orbital size
around the Sun.
- The Third Law was critical in determining the masses of other stars, using their orbits in binary star systems, and hence to deducing the physical processes that control stellar structure and evolution, one of the great accomplishments of 20th-century physics.
- The Third Law is applied today to such diverse astronomical problems as measuring the masses of "exoplanets" around other stars (see Study Guide 11) and establishing the existence of "Dark Matter" in distant galaxies.
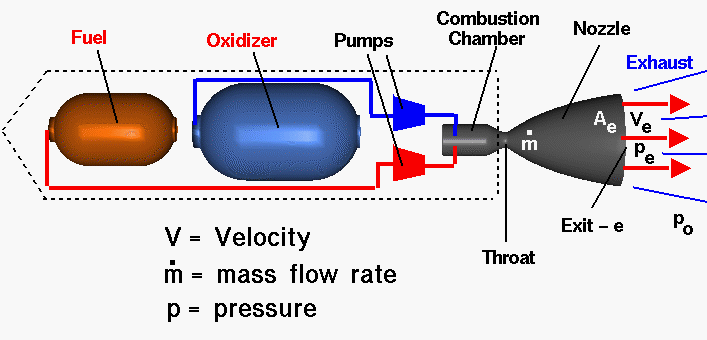
Schematic diagram of a liquid-fueled rocket engine.
Rockets carry both fuel and an oxidizer,
which allows the fuel to burn
even in the absence of an oxygen-rich atmosphere.
The thrust of the
engine is proportional to the velocity of the exhaust gases
(Ve).
C. Space Flight
If the primary technology enabling space flight is Newtonian orbit theory, the second most important technology is the rocket engine.
- In a rocket engine such as that shown in the diagram above, fuel
combined with oxidizer is burned rapidly in a combustion chamber and
converted into a large quantity of hot gas. The gas creates high
pressure, which causes it to be expelled out a nozzle at very high
velocity.
- The exhaust pressure
simultaneously forces the body of the rocket forward. You can think
of the rocket as "pushing off" from the moving molecules of exhaust
gas. The higher the exhaust velocity, the higher the thrust.
-
Note: rockets do not "push off" against the air or against the
Earth's surface. Rather, it is the "reaction force" between the
expelled exhaust and the rocket itself that impells the rocket forward.
- The main challenge to spaceflight is obtaining the power needed to
reach escape velocity. For Earth, this is 11 km/sec
or 25,000 mph.
-
The first successful launch of a
spacecraft, the
USSR's Sputnik-1, reached only 18,000 mph, but that was sufficient to
place this "artificial satellite" into an elliptical orbit around
Earth at several hundred miles altitude.
Modern "standard" rocket engines are designed for launching commercial
payloads to synchronous orbit or delivering intercontinental ballistic
missles---neither of which involve reaching escape velocity from
Earth. Therefore, most scientific spacecraft for planetary missions
are relatively small (i.e. low mass) in order that standard engines
can propel them past Earth escape velocity. This means that many
clever strategies are needed to pack high performance into small,
light packages.
- Example: The New Horizons
spacecraft, launched on a super-high velocity trajectory to Pluto in
2006, has a mass of only 1050 lbs; its launching rocket weighed
1,260,000 lbs, over 1000 times more! New Horizons flew past
Pluto in July 2015, traveling at over 34,000 mph, and has delivered a
treasure-trove of images and other data on this most distant (3
billion miles from Earth at the encounter) of the classical
planets.
A rocket launched at exactly escape velocity from a given parent body
will eventually, at very large distances, slow to exactly zero
velocity with respect to that body (ignoring the effect of other
gravitating bodies).
-
Modern rocket engines are remarkably
complicated. Here
is a simplified schematic of the Space Shuttle main engines.
D. Interplanetary Space Missions
Beginning in the early 1960's, NASA and foreign space agencies developed a series of ever-more sophisticated robot probes to study the Sun, Moon, planets, and the interplanetary medium. These included flyby spacecraft, orbiters, landers, rovers, and sample-return vehicles.
-
As of 2015, only 58 years after the first successful satellite launch
(Sputnik, in 1957), we had flown at close range past every planet
including Pluto; had placed robotic observatories into orbit around
the Moon, Mercury, Venus, Mars, Jupiter, Saturn, three asteroids, and
one comet; had sent probes into a comet nucleus and the atmosphere of
Jupiter; had soft-landed on the Moon, Venus, Mars, Saturn's moon
Titan, and the comet Churyumov-Gerasimenko; and had returned to Earth
samples obtained from the coma of the comet Wild 2 and from a
soft-landing on the asteroid Itokawa. And in 2013, the first human
spacecraft (Voyager-1) left the Solar System altogether and entered
interstellar space. At right is an artist's concept painting of
the Cassini mission in orbit around Saturn.
E. The Cost of Space Missions
Ever wonder why space flight is so expensive? It's because thousands of people are involved in almost any space endeavor, and it takes anywhere from 5 to 30 years to prepare a space mission. Spacecraft require not only their own launching and maneuvering engines but also command and control systems, power supplies, thermal control, pointing and stabilization systems, protection from a harsh environment, sensors and scientific instruments, data taking and storage systems, communications systems, and more -- all of these subject to stringent weight and volume constraints -- plus extensive Earth-based infrastructure to monitor and operate them. All those people are required in order to design and build these myriad components and then certify that they will be at least 95% reliable after launch --- because, with very few exceptions, no repair is possible. They must identify and mitigate all possible failure modes. Reliability is the principal cost driver of space missions. Needless to say, because of the demands of human safety, the cost of crewed missions greatly exceeds that of comparably-scaled robot missions. Two examples:- Wikipedia reports that "The Gemini 9A mission (a 1966, 3-day, low Earth orbit test flight with two astronauts) was supported by 11,301 personnel, 92 aircraft and 15 ships from the U.S. Department of Defense" -- not to mention thousands of NASA and private sector personnel.
- The Apollo Moon program involved a total of 410,000 people and 20,000 companies. Its $150 billion budget (in 2019 dollars) supported about 1,200,000 person-years of effort over 10 elapsed years -- the largest non-military project in history. For a modern overview of the scope and complexity of the Apollo program, see the recent book "One Giant Leap" by Charles Fishman. NASA's overall budget history is shown here. At its peak, the Apollo program accounted for over 4% of the total US federal budget.
- Apollo 11
Launch Video (ultra slo-mo, up-close-and-personal view of
a Saturn V launch)
or this:
Shuttle Discovery Prep to Launch (remarkable time-lapse video)

The Hubble Space Telescope on orbit 300 miles above Earth
Reading for this lecture:
- Bennett textbook: Ch. 4.1-4.4 (Newtonian dynamics &
gravitational orbits)
Study Guide 8
-
Study Guide 9 (this material is not covered in the text)
Web links:
-
Recommended interactive sites illustrating orbits:
-
Newton's Mountain (Java animation), from Mike Fowler's UVa Physics
course.
Gravity Chaos (Flash animation)--try to build multi-planet systems that don't self-destruct.
Newton's Laws & Rockets. (Also see other pages on aeronautics at this site.) JPL Notes on Basics of Space Flight History of Space Flight (James Schombert, Univ. of Oregon)
Wade's Encyclopedia of Astronautics
Complete list of current, planned, and past NASA science missions
NASA/Johnson Space Center Digital Image Collection Retrospective articles on 50 Years of the Space Race (New York Times)
The Apollo/Saturn V Moon rockets (the most powerful ever)
"Moon Machines - The Saturn V Rocket" documentary video Introduction to UV and Space Astronomy (O'Connell)
The Astro/Ultraviolet Imaging Telescope Missions(O'Connell)
Lecture on space observatories (O'Connell)
 Previous Guide
Previous Guide
|
 Guide Index
Guide Index
|
 Next Guide
Next Guide
|