ASTR 1230 (O'Connell) Lecture Notes

---

2. INTRODUCTION TO TELESCOPES

Summit of Mauna Kea, Hawaii, world's largest
astronomical observing complex

The telescope is the single most important invention for astronomy. Without it, we would have little of the profound understanding we have obtained over the last few hundred years about the physical nature of the universe and its history.

This lecture describes the main features of the design and operating principles of optical-band telescopes.

A. THE ELECTROMAGNETIC SPECTRUM

Maxwell (1865) discovered that electric and magnetic forces can propagate through space at the speed of light. The immediate inference was that light is an electromagnetic disturbance. The propagating disturbance moves through space like a wave through water and is called an electromagnetic ("EM") wave.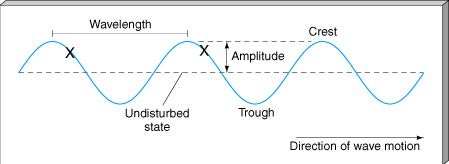

A wave disturbance

EM waves are characterized by their wavelengths, or the distance between peaks where the EM forces are strongest. All wavelengths from zero to infinity are possible for EM waves, and this total range is called the EM spectrum. From longest to shortest wavelengths, the EM spectrum includes: Radio, microwaves, infrared, optical light, ultraviolet light, X-rays, and gamma rays.

The human eye is directly sensitive only to a very small range of wavelengths in the EM spectrum. This is called the visible or optical region (see figure below). Within this region, the wavelength of the light determines the sensation of color produced in our eyes. Shorter wavelengths correspond to bluer colors.

• Wavelengths of optical light are conventionally measured in units of "Ångstroms" (where 1 Å = 10^-8 cm).

• The optical band extends roughly from wavelengths of 4000 Å in the deep violet to 7000 Å in the deep red. Green light has a wavelength around 5000 Å, or about 0.0005 mm---far smaller than sizes encountered in everyday life.

• Because the wavelength of optical light is so small, we are not conscious of light's wavelike character. But simple lab experiments quickly reveal that.

Full EM Spectrum with the Optical/Visible band enlarged
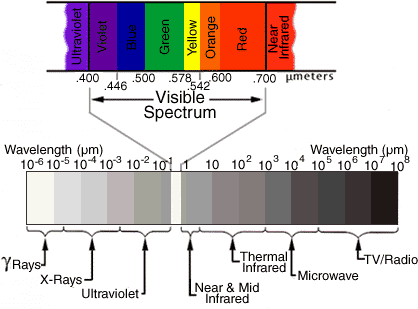
(Units marked are microns. 1 micron = 0.001 mm = 10^-4 cm = 10,000 Å)

Atmospheric "Windows"

The Earth's atmosphere is opaque to most wavelengths in the EM spectrum. This is a good thing for lifeforms on Earth's surface, because the more energetic types of EM radiation are harmful. But, obviously, it is not convenient for astronomers who want to monitor the universe across the full EM spectrum. (Eliminating atmospheric absorption is the main motivation for space astronomy.) The chart below shows the ability of different wavelengths to penetrate the atmosphere. The two main "atmospheric windows," where cosmic EM radiation can easily reach Earth's surface at sea level, are in the radio and optical bands. (Click for enlargement.)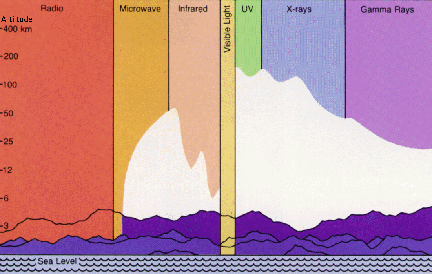

The rest of this lecture describes telescopes designed to work in the optical band. Telescopes in adjacent regions of the EM spectrum (the infrared and ultraviolet) are quite similar. But "telescopes" for the radio, X-ray, or gamma-ray bands are very different in design.

B. TELESCOPES: GENERAL

The telescope is a beautiful example of interplay between technology (fabrication of quality glass, polishing techniques, large mechanical structures, computers) and basic science.

History

• Invented: 1608 (Lipperhey, Holland). [Note: the microscope was also invented in Holland in the early 17th century.]

• First astronomical use: 1609, by (Galileo, Italy). Even though his telescopes were small (only 1-2 inch lenses) and crude by modern standards, they utterly transformed astronomy.
  • Galileo discovered, for instance, that there were thousands of stars too faint to be seen with the naked eye. His other important telescopic discoveries, which supported Copernicus' heliocentric model for the Solar System, are described here.

Purposes

• Collect more light from source
  This is the most important attribute of an astronomical telescope (because most astronomical sources are so faint)

• Magnify source
  "Magnify" means to make the source appear larger in angular size; this is the most important attribute of a terrestrial telescope but is less important for astronomical telescopes.

• Resolve more detail in source
  "Resolution" is distinct from magnification. A higher resolution image looks more sharp, less blurry, regardless of how large it is.

Basic Principle

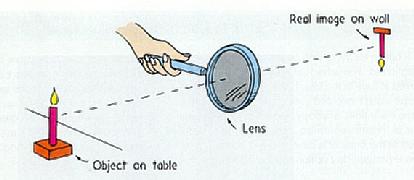
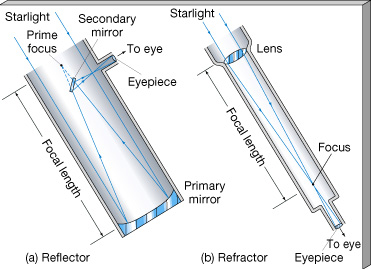
• An objective or primary optical element forms an image (i.e. an accurate representation of original scene) at a usable focus, where it can be studied by eye, recorded by film or other detectors (as in a camera), or fed into yet other instruments

Objectives: Two Types

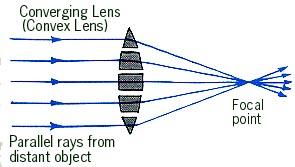
1. Lens: A lens is a piece transparent glass or plastic shaped to refract (or bend) light rays to a focus. The image at the left below shows how a flat glass surface bends light rays (in this case, two flat surfaces at an angle combine to make a prism). The shorter the wavelength (e.g. blue light), the stronger the bending. The image at the right shows how a glass surface can be continuously curved to bring all the light rays passing through it from a distant object to a common focal point. Each element of the lens acts like a small prism.

   Refraction of light by a prism (click for descriptive animation)	Shaped convex lens

   • Note that light rays travel in straight lines through empty space or through any medium (air, glass, water, etc) that has uniform properties. It is only at the boundaries between two uniform media that light rays can be deflected or "bent." The optical elements of a telescope therefore only change the directions of light rays at their surfaces (which represent glass/air boundaries).

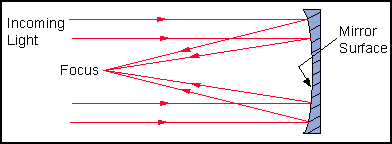
2. Mirror: A mirror is a shaped piece of glass which reflects light rays off its front surface to a common focus. A mirror shaped like a parabola will focus all rays that are parallel to its optical axis to a single point. See picture below.

Reflection of light by a figured mirror

Here is a video illustrating the differences between refraction, reflection, and diffraction.

• Note: Because the primary optical element is the most important part of a telescope, the "size" of a telescope is characterized by the diameter of its primary. The length of a telescope is not in direct proportion to its primary diameter but rather depends on the optical design.
  Thus, the "26-in" McCormick refracting telescope has a primary lens that is 26 inches in diameter. The "200-in" Palomar telescope has a primary mirror that is 200 inches in diameter.

Focal point

• For distant objects (including all astronomical objects), the incoming rays from each point on the source are parallel to each other. In this case, the image is formed at a position which is one focal length from the objective.
  • For nearer objects, the image is formed at a larger distance from the objective. Click on the button below for a Java applet illustrating image formation.

Applet

• Note that the image is inverted with respect to the original, as in the drawing below:
  

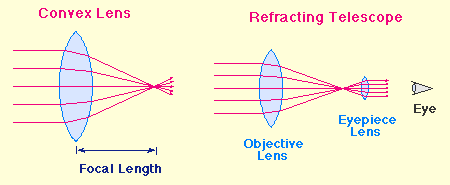
"Visual" Use

• In order to look through a telescope, a small lens called an eyepiece is used to magnify the image at the focal point and make the rays parallel again. This allows the eye to form a sharp image of it.
  (Although the lens of your eye is partially adjustable and can change its shape to focus on nearby or distant objects, the light beam from the objective of a telescope is converging or diverging too strongly to correct in the absence of an eyepiece.)

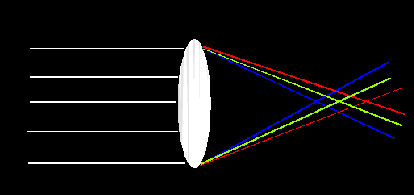
Aberrations

No optical system can produce a perfect image of a scene. Departures from a perfect image are called aberrations.
One important aberration for any refractive optical element is the fact that different wavelengths are deflected by different amounts (as shown in the prism animation above). In any refractive telescope (or eyepiece), this means that different colors of light come to a focus at different distances from the lens. See the illustration below. This is called chromatic aberration. You will experience it as a faint halo of color around any object viewed through your telescopes. Other aberrations are caused by the fact that no simple lens or mirror can precisely focus rays coming from different directions within the field of view to a single flat focal surface. Parabolic mirrors, for instance, produce a blur called coma that increases with off-axis angular distance. This kind of aberration can be reduced, but never completely eliminated, by using multi-mirror, multi-lens, or lens+mirror designs.
Light ray-traces of some important aberrations in mirrors can be found here.

C. CELESTRON TELESCOPES USED IN ASTR 1230

The telescopes you will use in this class are Celestron 8-in Schmidt-Cassegrain reflectors and use an equatorial fork-mount. This terminology is explained in the rest of the lecture.

A more complete description and full details on operation of the Celestrons are given in Chapter 3 of the ASTR 1230 Laboratory Manual.

D. TELESCOPE PERFORMANCE CHARACTERISTICS

Focal ratio or "f/ number"

• f/ = (Objective Focal Length)/(Objective Diameter).

• The smaller is the focal ratio, the more concentrated is the light in the focal plane and the easier it is to see faint extended objects like nebulae.
  [Same as for the aperture setting on a camera---the smaller the f/ number, the higher is the brightness in the focal plane.]

• Typical small telescopes have f/ numbers in the range 5-20. The Celestron 8-in telescopes are f/10 with focal lengths of 2032 mm.

Magnification or "power"

• Defined to be the fractional increase in the apparent angular size (measured, e.g., in degrees) of the image. With a "10x" or "10 power" telescope, a scene viewed through the telescope will appear to be 10 times larger in angular size than when viewed without the telescope.

• Mag = (Apparent Image Size in Degrees) / (Object Size Without Scope in Degrees).
  
• For a given telescope, magnification is inversely proportional to the focal length of the eyepiece:
  Mag = (Focal Length Telescope) / (Focal Length Eyepiece)
  For the Celestron 8-in scopes: Mag = 2032 mm/FLE. Thus:
  • A 40 mm eyepiece yields 50 power

  • A 20 mm eyepiece yields 100 power

  Note: high powers (> 150x) are not necessarily better, except for specialized applications (e.g. planets). High magnification is susceptible to image blurring by the atmosphere, telescope vibration, etc.

Field of View

• Defined to be the original angular diameter of the maximal region viewable through the telescope. Field of view decreases as magnification increases.

• E.g. with a 20 mm eyepiece, the Celestron 8-in scopes produce a field which is 20 minutes of arc in diameter. This is smaller than the angular diameter of the full Moon, which is 30 min of arc diameter. So you could not view the entire Moon through the telescope with a 20 mm eyepiece. However, you could do so with a 40 mm eyepiece.

Light Gathering Power

• Again, this is the most important attribute of a telescope

• Light collected is proportional to the area of the objective; think of the telescope as a "light bucket."
  The area of the objective is proportional to its diameter².

• Comparing the capability of the 8-in Celestron scope to the human eye:
  • Assume the pupil diameter of the dark-adapted eye is 5 mm. The Celestron objective is 203.2 mm.

  • The light gathering capability of the Celestron is therefore (203/5)² = (40)² = 1600x larger than your eye.

  • Therefore, with the telescope, you can see objects which are 1600x fainter than with your naked eye. If your eye can detect magnitude 5 stars, the Celestron will detect stars of 13th magnitude.
    There are over 5,000,000 of these, compared to the 2,000 or so visible with the naked eye!

  • For more information on the human eye as an astronomical detector, see this page.

Resolution: Optical Figuring Tolerance

• Resolution is quantitatively defined to be the smallest measurable detail in an image and is quoted in seconds of arc. In practice, this depends on your telescope's optics, the wave nature of light, and the Earth's atmosphere.

• To produce a good image, telescope optics must be fabricated to match their designed surface shape within a minimum tolerance of about 1/4 of a wavelength of light in their operating band. For optical telescopes, this is 10^-5 cm. Very small! -- but relatively easy to achieve with current technology.

• Scale comparison: if a 320-in (8-m) diameter telescope mirror (now a common size for a large professional facility) were scaled up to the size of the continental United States, i.e. about 3000 miles diameter, then the maximum size of a ripple allowed in its polishing would be about 2 inches!

• Good polishing/test techniques were not developed until the 19th century. To overcome limitations in optical technology, early astronomers favored telescopes with very long focal lengths (click here for an example), which reduced chromatic and spherical aberrations.

Resolution: Diffraction of Light Waves

• A fundamental limit to the resolution of any optical system is set by the physics of light: since it is a wave phenomenon, light spreads out or diffracts.
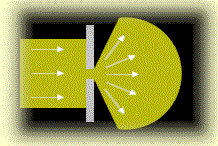
  Diffraction of light on passing
  through an aperture -- e.g. a telescope objective
  The picture above shows how light waves diffract when passing through an aperture, such as the objective lens of a telescope.
  Because of the interference of light waves from different parts of the aperture, the larger the aperture, the more concentrated the emerging beam, implying better resolution.

• The resolution is proportional to (Wavelength/Objective Diameter). The larger the telescope, the better the resolution.
  This picture illustrates the effects of telescope diameter on the size of the image of a binary star.
  (Note that all stars are so distant that they appear as point sources in smaller telescopes. You cannot actually detect any detail on star surfaces except in the largest telescopes).

• A 10-in diameter telescope with perfect optics will produce a 1 arc-sec diameter image of a star (assuming a perfectly stable atmosphere).

Resolution: Atmospheric "Seeing"

The Earth's atmosphere also refracts light, and because it is constantly moving, there is always a blurring and jittering of images in a telescope. Astronomers call this "seeing."
Local seeing (that near the telescope) is best if all nearby surfaces are at the same temperature as the air, because this minimizes turbulence created by local air currents. Modern professional observatories go to great lengths to minimize local seeing, basically by "airing out" the interior of telescope domes.
Quantitatively, seeing is defined to be the diameter of a star image (in seconds of arc) caused by atmospheric turbulence.
Expect typical seeing of 2-4 seconds of arc at the Student Observatory. Seeing can be measured by observing a double star of known separation (see writeup for Lab 3).
Except at good observing sites, seeing dominates diffraction in determining resolution in most cases, so having a better telescope often does not improve performance. Instead, you may need a better observing site.
Below is an enlarged image of the bright star Betelgeuse taken with a large telescope. It is a large blob, broken up into smaller near point-like units by seeing effects in the Earth's atmosphere. (The small "speckles" represent the image size you could see in the absence of atmospheric effects.) Click on the image for a video of the seeing effects. Click here and here for illustrations of seeing effects on observations of planets and the Moon.
"Seeing" in a star image produced
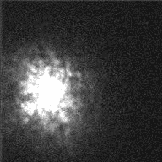
by turbulence in Earth's atmosphere

E. TELESCOPE TYPES

Three basic types of telescope optics

• Refracting: objective is a lens; bends rays. Examples: Galileo's telescopes; the McCormick 26-in.

• Reflecting: objective is a mirror; reflects rays. Invented by Gregory; improved by Newton. All large telescopes are reflectors.

• Catadioptric: combines lenses and mirrors, e.g. to produce a larger well defined field of view. Most famous: Schmidt wide field survey telescopes. These use a spherical primary mirror surface, which by itself would produce serious blurring but add a specially-shaped correcting lens at the front of the telescope that eliminates the blur.

Telescope Designs

A great variety! Here are four common types of reflector designs: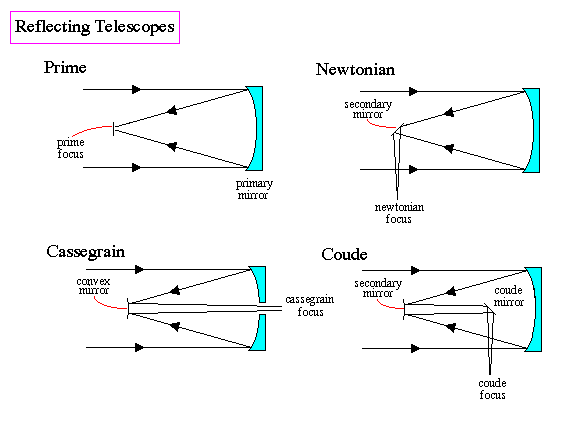

Note that in three of the designs shown, a "secondary" mirror at the top of the telescope tube is used to redirect the light beam. Although the secondary does block part beam falling on the primary, this has only a small effect on the net image quality. In particular, it does not produce a "hole" in the center of the image. In the Cassegrain design, a hole is actually made in the primary itself.
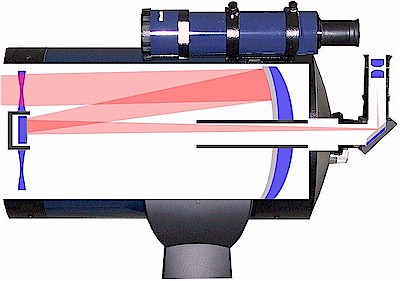
The Celestrons you will use are catadioptric systems. They combine a spherical mirror and Schmidt corrector plate with a Cassegrain through-the-primary light beam design. See diagram below:

Mounting designs

Again, a great variety. Two primary types:

• Altitude-Azimuth (Alt/Az) mount: one vertical axis and one horizontal axis. Easier to engineer, and therefore lower cost. But these require computer control for accurate tracking since the telescope must be moved in two axes simultaneously to follow stars. The popular, low-cost Dobsonian amateur telescopes have Alt-Az mountings (but without computers!).

• Equatorial mount: two axes, but polar axis is tilted to parallel the Earth's rotation axis. See this illustration. Motion around this one axis then tracks the stars as they move across the sky. Harder to engineer, easier to operate. Most telescopes use equatorial mounts but the largest ones are Alt-Az. Your Celestron 8-inch telescopes are fork-mounted equatorials.

Why are all large telescopes reflectors?

• Lenses produce chromatic aberration (see above). Since light of only a small range of wavelengths is in good focus, this is a particular difficulty for using modern broad-band electronic detectors.

• Mirrors need be figured only on one side

• Mirrors are easy to support accurately from behind; lenses require support at edges, tend to sag.

• It is harder to support a heavy lens mechanically at the top of a telescope tube than a mirror at the bottom.

• The folding action of primary and secondary mirrors means that reflector tubes are much shorter than in a "straight through" refracting design.

• For all these and other reasons, large reflectors are easier to design and cheaper to build than refractors and offer better performance in most applications.

Glass mirror blank for one of the two 8.4-m diameter
mirrors of the Large Binocular Telescope.

F. TELESCOPE MILESTONES

• Largest refractor: Yerkes 40-in (1896)

• Largest monolithic reflector: Large Binocular Telescope (one of its two mirrors is pictured above, each 8.4-m or 330 in; built 2005)

• Largest fully steerable reflectors (segmented): the Gran Telescopio Canarias (409 in: built 2009); and the twin Keck 10-m telescopes (395 in; built 1993).

• Here is a pictoral comparison of the mirror areas of the largest telescopes now existing and planned through 2030.

• For more information on modern professional telescopes, see Lecture Supplement 7.1.

G. BINOCULARS

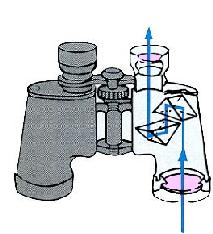A binocular is simply a pair of two small, co-aligned refracting telescopes mounted together in such a way that each eye can look through one of telescopes.

• Additional optics (prisms---see at right) are used so that the view is "right side up."

• The view for nearby objects is 3-dimensional; special optics may be used to increase the separation of the objective lenses for better 3-D resolution.

• Astronomical objects are so distant that there can be no 3-D effect. However, views with binoculars can be especially vivid because simultaneous use of both eyes reduces eye strain, and the optics of binoculars usually allow for easy centering of the eyes on the emergent beam. It is much easier to find your target with binoculars than with a telescope (assuming it's bright enough --- there is a big difference in limiting magnitude between binoculars and typical amateur telescopes).

• Binocular optics are usually classified in the form "7 x 35". Here, the first number is the net magnification of the binoculars, and the second is the diameter of the primary lenses in millimeters. Good types for general astronomical observations are 7x35 or 8x50. Binoculars higher than 10 power require tripods for stability. The field of view is also often marked on the binoculars, typically given as the diameter in feet for objects at a distance of 1000 yards.

• Binoculars can produce some of the best views of the Moon, rich star fields, comets, and the Milky Way.

Sunset over the William Herschel Telescope
(La Palma, Spain; N. Szymanek)

---

Assignment

• Download, print, and read the notes for Lecture 2.

• Take Review Quiz--Week 3 on the Collab site.

• Read Appendix C in the Manual on "Telescope Basics"

• Complete Lab 1 (Constellations) at either of the next two observing opportunities

• Begin Labs 2 (Introduction to Binoculars) and 3 (Introduction to Small Telescopes) as soon as possible after Lab 1. You do not have to complete Lab 2 before beginning Lab 3.
  Prepare for the Labs by carefully reading the writeups in the Manual.
  Read Appendices D and E on preparing lab reports and filling out observing forms.

Web links

Review of electromagnetic force and waves (O'Connell)
Early history of telescopes, with references.
More detailed notes on telescopes (Nick Strobel).
Tutorial on telescope and eyepiece design (Frosty Drew Observatory)
FAQ sheet for choosing amateur telescope equipment (D. Bishop)
Atmospheric Effects--Seeing & Extinction (M. Richmond)
Nice videos of seeing effects (P. van de Haar)
More on telescopes and modern observational astronomy (Lecture 7.1)
Introduction to detectors and astronomical color imaging (Lecture 7)
Celestron CPC 800 Instruction Manual (PDF)

---

Previous Lecture

Lecture Index

Next Lecture

Last modified December 2020 by rwo

---

Text copyright © 1998-2020 Robert W. O'Connell. All rights reserved. Some images copyright © by Prentice-Hall and by the University of Tennessee at Knoxville. WHT image copyright © by N. Szymanek. These notes are intended for the private, noncommercial use of students enrolled in Astronomy 1230 at the University of Virginia.